Jing Fang

Jing Fang (Chinese: 京房; pinyin: Jīng Fáng; Wade–Giles: Ching Fang, 78–37 BC), born Li Fang (李房), courtesy name Junming (君明), was born in present-day 東郡頓丘 (Puyang, Henan) during the Han Dynasty (202 BC – 220 AD). He was a Chinese music theorist, mathematician and astrologer.

Yijing

The historian Ban Gu (32–92 AD) wrote that Jing Fang was an expert at making predictions from the hexagrams of the ancient Yijing.^[1] A book on Yijing divination attributed to him describes the najia method of hexagram interpretation, which correlates their separate lines with elements of the Chinese calendar.^[2]

Music theory

According to the 3rd century historian Sima Biao, Jing Fang received an appointment as an official in the Music Bureau under Emperor Yuan of Han (r. 48–33 BC).^[1]

Jing Fang was the first to notice how closely a succession of 53 just fifths approximates 31 octaves. He came upon this observation after learning to calculate the pythagorean comma between 12 fifths and 7 octaves (this had been published ca. 122 BC in the Huainanzi, a book written for the prince of Huainan),^[3] and extended this method fivefold to a scale composed of 60 fifths, finding that after 53 new values became incredibly close to tones already calculated.

He accomplished this calculation by beginning with a suitable large starting value (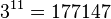)^[4] that could be divided by three easily, and proceeded to calculate the relative values of successive tones by the following method:

1. Divide the value by three.
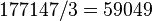
2. Add this value to the original.
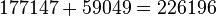
3. The new value is now equal to 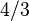of the original, or a perfect fourth, which is equivalent to a perfect fifth inverted at the octave. (Alternatively he would subtract 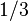from the interval, equivalent to a perfect fifth down, in order to keep all of the values greater than 177147, or less than 354294, its double, effectively transposing them all into the range of a single octave.)
4. Proceed now from this new value to generate the next tone; repeat until all tones have been generated.

To produce an exact calculation, some 26 digits of accuracy would have been required.^[5] Instead, by rounding to about 6 digits, his calculations are within 0.0145 cents of exactness, which is a difference much finer than is usually perceptible. The final value he gave for the ratio between this 53rd fifth and the original was —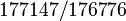.^[5]

This value would later be calculated precisely by Nicholas Mercator in the 17th century (see: history of 53 equal temperament).

Astronomy

He was also an advocate of the theory that the light emanating from the spherical Moon (as seen from Earth) was merely a reflection of sunlight. This was known as the 'radiating influence' theory in ancient China, which stated that the light of the moon was merely the light reflected from the sun, and that the celestial bodies were spherical. This accurate theory was dismissed by the philosopher Wang Chong (27–97 AD), yet embraced by the mathematician, inventor and scientist Zhang Heng (78–139 AD).

Jing Fang stated:

Death

It is recorded that he was executed by beheading in the marketplace in 37 BC under the Emperor's orders after he allegedly slung false accusations at a high official for infringing upon the law.^[1]

See also

• Wen Wang Gua

Notes

References

• Huang, Xiangpeng, "Jing Fang". Encyclopedia of China (Music and Dance Edition), 1st ed.
• McClain, Ernest and Ming Shui Hung. "Chinese Cyclic Tunings in Late Antiquity," Ethnomusicology, Vol. 23, No. 2 (1979): 205-224.
• Needham, Joseph (1986). Science and Civilization in China: Volume 3, Mathematics and the Sciences of the Heavens and the Earth. Taipei: Caves Books, Ltd.
• Complete table of Jing Fangs hexagram values: Jing Fang Hexagram Table