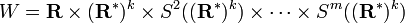Jet group

From Wikipedia, the free encyclopedia

In mathematics, a jet group is a generalization of the general linear group which applies to Taylor polynomials instead of vectors at a point. Essentially a jet group describes how a Taylor polynomial transforms under changes of coordinate systems (or, equivalently, diffeomorphisms).

The k-th order jet group Gⁿ_k consists of jets of smooth diffeomorphisms φ: Rⁿ → Rⁿ such that φ(0)=0.

The following is a more precise definition of the jet group.

Let k ≥ 2. The gradient of a function f: R^k → R can be interpreted as a section of the cotangent bundle of R^K given by df: R^k → T*R^k. Similarly, derivatives of order up to m are sections of the jet bundle J^m(R^k) = R^k × W, where

$W={\mathbf R}\times ({\mathbf R}^{*})^{k}\times S^{2}(({\mathbf R}^{*})^{k})\times \cdots \times S^{{m}}(({\mathbf R}^{*})^{k})$

and Sⁱ denotes the i-th symmetric power. A function f: R^k → R has a prolongation j^mf: Rⁿ → J^m(Rⁿ) defined at each point p ∈ R^k by placing the i-th partials of f at p in the Sⁱ((R*)^k) component of W.

Consider a point 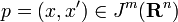$p=(x,x')\in J^{m}({\mathbf R}^{n})$ . There is a unique polynomial f_p in k variables and of order m such that p is in the image of j^mf_p. That is, 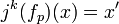$j^{k}(f_{p})(x)=x'$ . The differential data x′ may be transferred to lie over another point y ∈ Rⁿ as j^mf_p(y) , the partials of f_p over y.

Provide J^m(Rⁿ) with a group structure by taking

$(x,x')*(y,y')=(x+y,j^{m}f_{p}(y)+y')$

With this group structure, J^m(Rⁿ) is a Carnot group of class m + 1.

Because of the properties of jets under function composition, Gⁿ_k is a Lie group. The jet group is a semidirect product of the general linear group and a connected, simply connected nilpotent Lie group. It is also in fact an algebraic group, since the composition involves only polynomial operations.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.