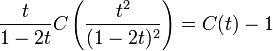Jacques Touchard

From Wikipedia, the free encyclopedia

Jacques Touchard (1885 – 1968) was a French mathematician. In 1953, he proved that an odd perfect number must be of the form 12k + 1 or 36k + 9. In combinatorics and probability theory, he introduced the Touchard polynomials. He is also known for his solution to the ménage problem of counting seating arrangements in which men and women alternate and are not seated next to their spouses.

Touchard's Catalan identity

The following algebraic identity involving the Catalan numbers

$C_{k}={1 \over {k+1}}{{2k} \choose {k}},\quad k\geq 0$

is apparently due to Touchard (according to Richard P. Stanley, who mentions it in his panorama article "Exercises on Catalan and Related Numbers" giving an overwhelming plenitude of different definitions for the Catalan numbers). For n ≥ 0 one has

$C_{{n+1}}=\sum _{{k\,\leq \,n/2}}2^{{n-2k}}{n \choose 2k}C_{k}.\,$

Using the generating function

$C(t)=\sum _{{n\geq 0}}C_{n}t^{n}={{1-{\sqrt {1-4t}}} \over {2t}}$

it can be proved by algebraic manipulations of generating series that Touchard's identity is equivalent to the functional equation

${t \over {1-2t}}C\left({t^{2} \over (1-2t)^{2}}\right)=C(t)-1$

satisfied by the Catalan generating series C(t).

Persondata
Name	Touchard, Jacques
Alternative names
Short description	French mathematician
Date of birth	1885
Place of birth
Date of death	1968
Place of death

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.