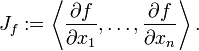Jacobian ideal

From Wikipedia, the free encyclopedia

In mathematics the Jacobian ideal or gradient ideal is the ideal generated by the Jacobian of a function or function germ. Let 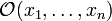{\mathcal {O}}(x_{1},\ldots ,x_{n}) denote the ring of smooth functions and f a function in the ring. The Jacobian ideal of f is

J_{f}:=\left\langle {\frac {\partial f}{\partial x_{1}}},\ldots ,{\frac {\partial f}{\partial x_{n}}}\right\rangle .

See also


This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.