Jacobi polynomials
In mathematics, Jacobi polynomials (occasionally called hypergeometric polynomials) Pn(α, β)(x) are a class of classical orthogonal polynomials. They are orthogonal with respect to the weight (1 - x)α(1 + x)β on the interval [-1, 1]. The Gegenbauer polynomials, and thus also the Legendre, Zernike and Chebyshev polynomials, are special cases of the Jacobi polynomials.[1]
The Jacobi polynomials were introduced by Carl Gustav Jacob Jacobi.
Definitions
Via the hypergeometric function
The Jacobi polynomials are defined via the hypergeometric function as follows:[2]
where 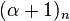 is Pochhammer's symbol (for the rising factorial). In this case, the series for the hypergeometric function is finite, therefore one obtains the following equivalent expression:
is Pochhammer's symbol (for the rising factorial). In this case, the series for the hypergeometric function is finite, therefore one obtains the following equivalent expression:
Rodrigues' formula
An equivalent definition is given by Rodrigues' formula:[1][3]
Alternate expression for real argument
For real x the Jacobi polynomial can alternatively be written as
where s ≥ 0 and n−s ≥ 0, and for integer n
and Γ(z) is the Gamma function, using the convention that:
In the special case that the four quantities n, n+α, n+β, and n+α+β are nonnegative integers, the Jacobi polynomial can be written as
-
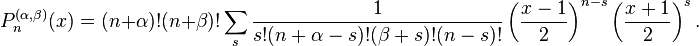
(1)
The sum extends over all integer values of s for which the arguments of the factorials are nonnegative.
Basic properties
Orthogonality
The Jacobi polynomials satisfy the orthogonality condition
for α, β > −1.
As defined, they are not orthonormal, the normalization being
Symmetry relation
The polynomials have the symmetry relation
thus the other terminal value is
Derivatives
The kth derivative of the explicit expression leads to
Differential equation
The Jacobi polynomial Pn(α, β) is a solution of the second order linear homogeneous differential equation[1]
Recurrence relation
The recurrent relation for the Jacobi polynomials is:[1]
for n = 2, 3, ....
Generating function
The generating function of the Jacobi polynomials is given by
where
and the branch of square root is chosen so that R(z, 0) = 1.[1]
Asymptotics of Jacobi polynomials
For x in the interior of [-1, 1], the asymptotics of Pn(α, β) for large n is given by the Darboux formula[1]
where
and the "O" term is uniform on the interval [ε, π-ε] for every ε > 0.
The asymptotics of the Jacobi polynomials near the points ±1 is given by the Mehler–Heine formula
where the limits are uniform for z in a bounded domain.
The asymptotics outside [−1, 1] is less explicit.
Applications
Wigner d-matrix
The expression (1) allows the expression of the Wigner d-matrix djm’,m(φ) (for 0 ≤ φ ≤ 4π) in terms of Jacobi polynomials:[4]
See also
- Askey–Gasper inequality
- Big q-Jacobi polynomials
- Continuous q-Jacobi polynomials
- Little q-Jacobi polynomials
- Pseudo Jacobi polynomials
- Jacobi process
Notes
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 Szegő, Gábor (1939). "IV. Jacobi polynomials.". Orthogonal Polynomials. Colloquium Publications. XXIII. American Mathematical Society. ISBN 978-0-8218-1023-1. MR 0372517. The definition is in IV.1; the differential equation – in IV.2; Rodrigues' formula is in IV.3; the generating function is in IV.4; the recurrent relation is in IV.5.
- ↑ Abramowitz, Milton; Stegun, Irene A., eds. (1965), "Chapter 22", Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover, p. 561, ISBN 978-0486612720, MR 0167642.
- ↑ P.K. Suetin (2001), "Jacobi_polynomials", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- ↑ Biedenharn, L.C.; Louck, J.D. (1981). Angular Momentum in Quantum Physics. Reading: Addison-Wesley.
Further reading
- Andrews, George E.; Askey, Richard; Roy, Ranjan (1999), Special functions, Encyclopedia of Mathematics and its Applications 71, Cambridge University Press, ISBN 978-0-521-62321-6; 978-0-521-78988-2 Check
|isbn=value (help), MR 1688958 - Koornwinder, Tom H.; Wong, Roderick S. C.; Koekoek, Roelof; Swarttouw, René F. (2010), "Orthogonal Polynomials", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR 2723248
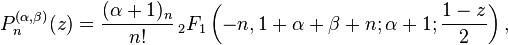
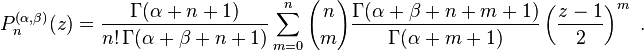
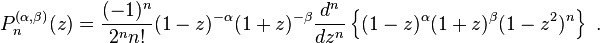

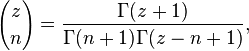
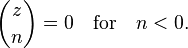
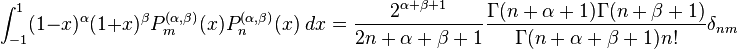
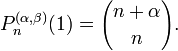
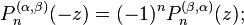
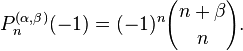




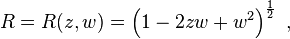
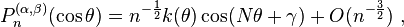

![{\begin{aligned}\lim _{{n\to \infty }}n^{{-\alpha }}P_{n}^{{(\alpha ,\beta )}}\left(\cos {\frac {z}{n}}\right)&=\left({\frac {z}{2}}\right)^{{-\alpha }}J_{\alpha }(z)~,\\\lim _{{n\to \infty }}n^{{-\beta }}P_{n}^{{(\alpha ,\beta )}}\left(\cos \left[\pi -{\frac {z}{n}}\right]\right)&=\left({\frac {z}{2}}\right)^{{-\beta }}J_{\beta }(z)~,\end{aligned}}](/2014-wikipedia_en_all_02_2014/I/media/2/3/a/a/23aaab33b3bbf464397db511e50d1bc8.png)
![d_{{m'm}}^{j}(\phi )=\left[{\frac {(j+m)!(j-m)!}{(j+m')!(j-m')!}}\right]^{{{\frac {1}{2}}}}\left(\sin {\frac {\phi }{2}}\right)^{{m-m'}}\left(\cos {\frac {\phi }{2}}\right)^{{m+m'}}P_{{j-m}}^{{(m-m',m+m')}}(\cos \phi ).](/2014-wikipedia_en_all_02_2014/I/media/e/f/b/6/efb657ad43072eb437133fa143cb3d2b.png)