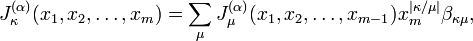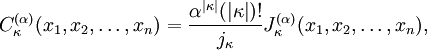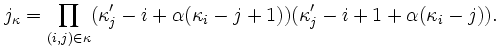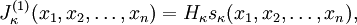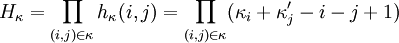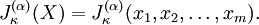Jack function

From Wikipedia, the free encyclopedia

In mathematics, the Jack function, introduced by Henry Jack, is a homogenous, symmetric polynomial which generalizes the Schur and zonal polynomials, and is in turn generalized by the Heckman–Opdam polynomials and Macdonald polynomials.

Definition

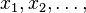The Jack function $J_{\kappa }^{{(\alpha )}}(x_{1},x_{2},\ldots ,x_{m})$ of integer partition $\kappa$ , parameter $\alpha$ and arguments $x_{1},x_{2},\ldots ,$ can be recursively defined as follows:

For m=1

$J_{{k}}^{{(\alpha )}}(x_{1})=x_{1}^{k}(1+\alpha )\cdots (1+(k-1)\alpha )$

For m>1

$J_{\kappa }^{{(\alpha )}}(x_{1},x_{2},\ldots ,x_{m})=\sum _{\mu }J_{\mu }^{{(\alpha )}}(x_{1},x_{2},\ldots ,x_{{m-1}})x_{m}^{{|\kappa /\mu |}}\beta _{{\kappa \mu }},$

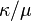where the summation is over all partitions $\mu$ such that the skew partition $\kappa /\mu$ is a horizontal strip, namely

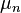$\kappa _{1}\geq \mu _{1}\geq \kappa _{2}\geq \mu _{2}\geq \cdots \geq \kappa _{{n-1}}\geq \mu _{{n-1}}\geq \kappa _{n}$ ( $\mu _{n}$ must be zero or otherwise $J_{\mu }(x_{1},\ldots ,x_{{n-1}})=0$ ) and

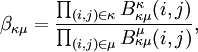
$\beta _{{\kappa \mu }}={\frac {\prod _{{(i,j)\in \kappa }}B_{{\kappa \mu }}^{\kappa }(i,j)}{\prod _{{(i,j)\in \mu }}B_{{\kappa \mu }}^{\mu }(i,j)}},$

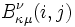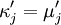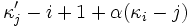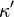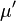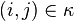where $B_{{\kappa \mu }}^{\nu }(i,j)$ equals $\kappa _{j}'-i+\alpha (\kappa _{i}-j+1)$ if $\kappa _{j}'=\mu _{j}'$ and $\kappa _{j}'-i+1+\alpha (\kappa _{i}-j)$ otherwise. The expressions $\kappa '$ and $\mu '$ refer to the conjugate partitions of $\kappa$ and $\mu$ , respectively. The notation $(i,j)\in \kappa$ means that the product is taken over all coordinates 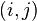$(i,j)$ of boxes in the Young diagram of the partition $\kappa$ .

C normalization

The Jack functions form an orthogonal basis in a space of symmetric polynomials, with inner product: $\langle f,g\rangle =\int _{{[0,2\pi ]^{n}}}f(e^{{i\theta _{1}}},\cdots ,e^{{i\theta _{n}}})\overline {g(e^{{i\theta _{1}}},\cdots ,e^{{i\theta _{n}}})}\prod _{{1\leq j<k\leq n}}|e^{{i\theta _{j}}}-e^{{i\theta _{k}}}|^{{2/\alpha }}d\theta _{1}\cdots d\theta _{n}$

This orthogonality property is unaffected by normalization. The normalization defined above is typically referred to as the J normalization. The C normalization is defined as

$C_{\kappa }^{{(\alpha )}}(x_{1},x_{2},\ldots ,x_{n})={\frac {\alpha ^{{|\kappa |}}(|\kappa |)!}{j_{\kappa }}}J_{\kappa }^{{(\alpha )}}(x_{1},x_{2},\ldots ,x_{n}),$

where

$j_{\kappa }=\prod _{{(i,j)\in \kappa }}(\kappa _{j}'-i+\alpha (\kappa _{i}-j+1))(\kappa _{j}'-i+1+\alpha (\kappa _{i}-j)).$

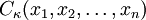For $\alpha =2,\;C_{\kappa }^{{(2)}}(x_{1},x_{2},\ldots ,x_{n})$ denoted often as just $C_{\kappa }(x_{1},x_{2},\ldots ,x_{n})$ is known as the Zonal polynomial.

Connection with the Schur polynomial

When 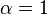$\alpha =1$ the Jack function is a scalar multiple of the Schur polynomial

$J_{\kappa }^{{(1)}}(x_{1},x_{2},\ldots ,x_{n})=H_{\kappa }s_{\kappa }(x_{1},x_{2},\ldots ,x_{n}),$

where

$H_{\kappa }=\prod _{{(i,j)\in \kappa }}h_{\kappa }(i,j)=\prod _{{(i,j)\in \kappa }}(\kappa _{i}+\kappa _{j}'-i-j+1)$

is the product of all hook lengths of $\kappa$ .

Properties

If the partition has more parts than the number of variables, then the Jack function is 0:

$J_{\kappa }^{{(\alpha )}}(x_{1},x_{2},\ldots ,x_{m})=0,{\mbox{ if }}\kappa _{{m+1}}>0.$

Matrix argument

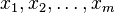In some texts, especially in random matrix theory, authors have found it more convenient to use a matrix argument in the Jack function. The connection is simple. If $X$ is a matrix with eigenvalues $x_{1},x_{2},\ldots ,x_{m}$ , then

$J_{\kappa }^{{(\alpha )}}(X)=J_{\kappa }^{{(\alpha )}}(x_{1},x_{2},\ldots ,x_{m}).$

References

Demmel, James; Koev, Plamen (2006), "Accurate and efficient evaluation of Schur and Jack functions", Mathematics of Computation 75 (253): 223–239, doi:10.1090/S0025-5718-05-01780-1, MR 2176397 .
Jack, Henry (1970–1971), "A class of symmetric polynomials with a parameter", Proceedings of the Royal Society of Edinburgh, Section A. Mathematics 69: 1–18, MR 0289462 Check date values in: |date= (help).
Macdonald, I. G. (1995), Symmetric functions and Hall polynomials, Oxford Mathematical Monographs (2nd ed.), New York: Oxford University Press, ISBN 0-19-853489-2, MR 1354144
Stanley, Richard P. (1989), "Some combinatorial properties of Jack symmetric functions", Advances in Mathematics 77 (1): 76–115, doi:10.1016/0001-8708(89)90015-7, MR 1014073 .

External links

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.