J-invariant

In mathematics, Klein's j-invariant, regarded as a function of a complex variable τ, is a modular function of weight zero for 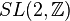 defined on the upper half-plane of complex numbers. It is the unique such function which is holomorphic away from a simple pole at the cusp such that
defined on the upper half-plane of complex numbers. It is the unique such function which is holomorphic away from a simple pole at the cusp such that 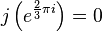 and
and 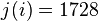 . Rational functions of
. Rational functions of  are modular, and in fact give all modular functions. Classically, the j-invariant was studied as a parameterization of elliptic curves over
are modular, and in fact give all modular functions. Classically, the j-invariant was studied as a parameterization of elliptic curves over  , but it also has surprising connections to the symmetries of the Monster group (this connection is referred to as monstrous moonshine).
, but it also has surprising connections to the symmetries of the Monster group (this connection is referred to as monstrous moonshine).
Definition


While the j-invariant can be defined purely in terms of certain infinite sums (see  below), these can be motivated by considering isomorphism classes of elliptic curves. Every elliptic curve
below), these can be motivated by considering isomorphism classes of elliptic curves. Every elliptic curve  over
over  is a complex torus, and thus can be identified with a rank 2 lattice; i.e., two-dimensional lattice of
is a complex torus, and thus can be identified with a rank 2 lattice; i.e., two-dimensional lattice of  . This is done by identifying opposite edges of each parallelogram in the lattice. It turns out that multiplying the lattice by complex numbers, which corresponds to rotating and scaling the lattice, preserves the isomorphism class of the elliptic curve, and thus we can consider the lattice generated by 1 and some
. This is done by identifying opposite edges of each parallelogram in the lattice. It turns out that multiplying the lattice by complex numbers, which corresponds to rotating and scaling the lattice, preserves the isomorphism class of the elliptic curve, and thus we can consider the lattice generated by 1 and some  (where
(where  is the Upper half-plane). Conversely, if we define
is the Upper half-plane). Conversely, if we define
then this lattice corresponds to the elliptic curve over  defined by
defined by 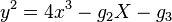 via the Weierstrass elliptic functions. Then the j-invariant is defined as
via the Weierstrass elliptic functions. Then the j-invariant is defined as
where the modular discriminant  is
is
It can be shown that  is a modular form of weight twelve, and
is a modular form of weight twelve, and 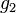 one of weight four, so that its third power is also of weight twelve. Thus their quotient, and therefore
one of weight four, so that its third power is also of weight twelve. Thus their quotient, and therefore  , is a modular function of weight zero, in particular a meromorphic function
, is a modular function of weight zero, in particular a meromorphic function 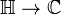 invariant under the action of
invariant under the action of 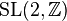 . As explained below,
. As explained below,  is surjective, which means that it gives a bijection between isomorphism classes of elliptic curves over
is surjective, which means that it gives a bijection between isomorphism classes of elliptic curves over  and the complex numbers.
and the complex numbers.
The fundamental region

The two transformations τ → τ + 1 and τ → τ−1 together generate a group called the modular group, which we may identify with the projective special linear group  . By a suitable choice of transformation belonging to this group, τ → (aτ + b)/(cτ + d), with ad − bc = 1, we may reduce τ to a value giving the same value for j, and lying in the fundamental region for j, which consists of values for τ satisfying the conditions
. By a suitable choice of transformation belonging to this group, τ → (aτ + b)/(cτ + d), with ad − bc = 1, we may reduce τ to a value giving the same value for j, and lying in the fundamental region for j, which consists of values for τ satisfying the conditions
The function j(τ) when restricted to this region still takes on every value in the complex numbers  exactly once. In other words, for every
exactly once. In other words, for every 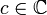 , there is a unique τ in the fundamental region such that c=j(τ). Thus, j has the property of mapping the fundamental region to the entire complex plane.
, there is a unique τ in the fundamental region such that c=j(τ). Thus, j has the property of mapping the fundamental region to the entire complex plane.
As a Riemann surface, the fundamental region has genus 0, and every (level one) modular function is a rational function in j; and, conversely, every rational function in j is a modular function. In other words the field of modular functions is 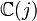 .
.
Class field theory and j
The j-invariant has many remarkable properties. One of these is that if τ is any of the singular moduli, that is, any element of an imaginary quadratic field with positive imaginary part (so that j is defined) then  is an algebraic integer.[1] The field extension
is an algebraic integer.[1] The field extension
is abelian, meaning with abelian Galois group. We have a lattice in the complex plane defined by 1 and τ, and it is easy to see that all of the elements of the field  which send lattice points to other lattice points under multiplication form a ring with units, called an order. The other lattices with generators 1 and τ' associated in like manner to the same order define the algebraic conjugates
which send lattice points to other lattice points under multiplication form a ring with units, called an order. The other lattices with generators 1 and τ' associated in like manner to the same order define the algebraic conjugates  of
of  over
over  . The unique maximal order under inclusion of
. The unique maximal order under inclusion of  is the ring of algebraic integers of
is the ring of algebraic integers of  , and values of τ having it as its associated order lead to unramified extensions of
, and values of τ having it as its associated order lead to unramified extensions of  . These classical results are the starting point for the theory of complex multiplication.
. These classical results are the starting point for the theory of complex multiplication.
Transcendence properties
In 1937 Theodor Schneider proved the aforementioned result that if  is a quadratic irrational number in the upper half plane then j(
is a quadratic irrational number in the upper half plane then j( ) is an algebraic integer. In addition he proved that if
) is an algebraic integer. In addition he proved that if  is an algebraic number but not imaginary quadratic then j(
is an algebraic number but not imaginary quadratic then j( ) is transcendental.
) is transcendental.
The j function has numerous other transcendental properties. Kurt Mahler conjectured a particular transcendence result that is often referred to as Mahler's conjecture, though it was proved as a corollary of results by Yu. V. Nesternko and Patrice Phillipon in the 1990s. Mahler's conjecture was that the if  was in the upper half plane then exp(2πi
was in the upper half plane then exp(2πi ) and j(
) and j( ) were never both simultaneously algebraic. Stronger results are now known, for example if exp(2πi
) were never both simultaneously algebraic. Stronger results are now known, for example if exp(2πi ) is algebraic then the following three numbers are algebraically independent, and thus transcendental:
) is algebraic then the following three numbers are algebraically independent, and thus transcendental:
The q-expansion and moonshine
Several remarkable properties of j have to do with its q-expansion (Fourier series expansion, written as a Laurent series in terms of q= exp(2πiτ)), which begins:
Note that j has a simple pole at the cusp, so its q-expansion has no terms below q−1.
All the Fourier coefficients are integers, which results in several almost integers, notably Ramanujan's constant: 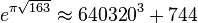 .
.
Moonshine
More remarkably, the Fourier coefficients for the positive exponents of q are the dimensions of the graded part of an infinite-dimensional graded algebra representation of the monster group called the moonshine module – specifically, the coefficient of  is the dimension of grade-n part of the moonshine module, the first example being the Griess algebra, which has dimension 196,884, corresponding to the term
is the dimension of grade-n part of the moonshine module, the first example being the Griess algebra, which has dimension 196,884, corresponding to the term 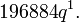 This startling observation was the starting point for moonshine theory.
This startling observation was the starting point for moonshine theory.
The study of the Moonshine conjecture led J.H. Conway and Simon P. Norton to look at the genus-zero modular functions. If they are normalized to have the form
then Thompson showed that there are only a finite number of such functions (of some finite level), and Cummins later showed that there are exactly 6486 of them, 616 of which have integral coefficients.[2]
Alternate Expressions
We have
where 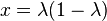 and
and 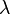 is the modular lambda function. The value of j is unchanged when λ is replaced by any of the six values of the cross-ratio:[3]
is the modular lambda function. The value of j is unchanged when λ is replaced by any of the six values of the cross-ratio:[3]
The branch points of j are at {0,1,∞}, so that j is a Belyi function.[4]
Expressions in terms of theta functions
We can express it in terms of Jacobi's theta functions, in which form it can very rapidly be computed.
Algebraic definition
So far we have been considering j as a function of a complex variable. However, as an invariant for isomorphism classes of elliptic curves, it can be defined purely algebraically. Let
be a plane elliptic curve over any field. Then we may define
and
the latter expression is the discriminant of the curve.
The j-invariant for the elliptic curve may now be defined as
In the case that the field over which the curve is defined has characteristic different from 2 or 3, this definition can also be written as
Inverse and special values
The inverse function of the j-invariant can be expressed in terms of the hypergeometric function  (see also the article Picard–Fuchs equation). Explicitly, to solve for
(see also the article Picard–Fuchs equation). Explicitly, to solve for  in the equation,
in the equation,
when N is known, let  be any root of the quadratic,
be any root of the quadratic,
then,
One root gives τ, and the other gives 1/τ, but since  , then it doesn't make a difference which
, then it doesn't make a difference which  is chosen. Alternatively, recall that,
is chosen. Alternatively, recall that,
where 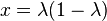 and
and 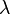 is the modular lambda function. As an unknown, one can find
is the modular lambda function. As an unknown, one can find 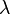 by solving the cubic in x, then the quadratic. Then,
by solving the cubic in x, then the quadratic. Then,
for any of the six values of 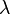 . The inversion is highly relevant to applications via enabling high-precision calculations of elliptic functions periods even as their ratios become unbounded. A related result is the expressibility via quadratic radicals of the values of j at the points of the imaginary axis whose magnitudes are powers of 2 (thus permitting compass and straightedge constructions). The latter result is hardly evident since the modular equation of level 2 is cubic.
. The inversion is highly relevant to applications via enabling high-precision calculations of elliptic functions periods even as their ratios become unbounded. A related result is the expressibility via quadratic radicals of the values of j at the points of the imaginary axis whose magnitudes are powers of 2 (thus permitting compass and straightedge constructions). The latter result is hardly evident since the modular equation of level 2 is cubic.
The j-invariant vanishes at the "corner" of the fundamental domain at 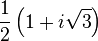 . Here are a few more special values (only the first four of which are well known; in what follows, j means J/1728 throughout):
. Here are a few more special values (only the first four of which are well known; in what follows, j means J/1728 throughout):
References
- ↑ Silverman, Joseph H. (1986). The Arithmetic of Elliptic Curves. Graduate Texts in Mathematics 106. Springer-Verlag. p. 339. ISBN 0-387-96203-4. Zbl 0585.14026.
- ↑ Cummins, C.J. (2004). "Congruence subgroups of groups commensurable with PSL(2,Z)$ of genus 0 and 1". Exp. Math. 13 (3): 361–382. ISSN 1058-6458. Zbl 1099.11022.
- ↑ Chandrasekharan, K. (1985), Elliptic Functions, Grundlehren der mathematischen Wissenschaften 281, Springer-Verlag, p. 110, ISBN 3-540-15295-4, Zbl 0575.33001
- ↑ Girondo, Ernesto; González-Diez, Gabino (2012), Introduction to compact Riemann surfaces and dessins d'enfants, London Mathematical Society Student Texts 79, Cambridge: Cambridge University Press, p. 267, ISBN 978-0-521-74022-7, Zbl 1253.30001
- Apostol, Tom M. (1976), Modular functions and Dirichlet Series in Number Theory, Graduate Texts in Mathematics 41, New York: Springer-Verlag, MR 0422157. Provides a very readable introduction and various interesting identities.
- Apostol, Tom M. (1990), Modular functions and Dirichlet Series in Number Theory (2nd ed.), ISBN 0-387-97127-0, MR 1027834
- Berndt, Bruce C.; Chan, Heng Huat (1999), "Ramanujan and the modular j-invariant", Canadian Mathematical Bulletin 42 (4): 427–440, doi:10.4153/CMB-1999-050-1, MR 1727340. Provides a variety of interesting algebraic identities, including the inverse as a hypergeometric series.
- Cox, David A. (1989), Primes of the Form x^2 + ny^2: Fermat, Class Field Theory, and Complex Multiplication, New York: Wiley-Interscience Publication, John Wiley & Sons Inc., MR 1028322 Introduces the j-invariant and discusses the related class field theory.
- Conway, John Horton; Norton, Simon (1979), "Monstrous moonshine", Bulletin of the London Mathematical Society 11 (3): 308–339, doi:10.1112/blms/11.3.308, MR 0554399. Includes a list of the 175 genus-zero modular functions.
- Petersson, Hans (1932), "Über die Entwicklungskoeffizienten der automorphen Formen", Acta Mathematica 58 (1): 169–215, doi:10.1007/BF02547776, MR 1555346.
- Rademacher, Hans (1938), "The Fourier coefficients of the modular invariant j(τ)", American Journal of Mathematics (The Johns Hopkins University Press) 60 (2): 501–512, doi:10.2307/2371313, JSTOR 2371313, MR 1507331.
- Rankin, Robert A. (1977), Modular forms and functions, Cambridge: Cambridge University Press, ISBN 0-521-21212-X, MR 0498390. Provides a short review in the context of modular forms.
- Schneider, Theodor (1937), "Arithmetische Untersuchungen elliptischer Integrale", Math. Annalen 113: 1–13, doi:10.1007/BF01571618, MR 1513075.
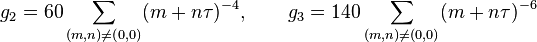
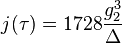
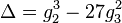
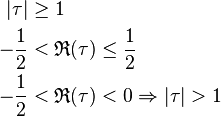
![{\mathbb {Q}}[j(\tau ),\tau ]/{\mathbb {Q}}(\tau )](/2014-wikipedia_en_all_02_2014/I/media/f/0/3/b/f03bbbe8bccaccbc310518259ead9ff9.png)
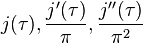
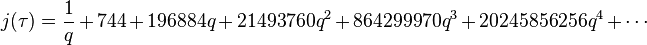
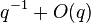
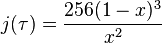

![g_{2}(\tau )={2\pi ^{4} \over 3}\left[\vartheta (0;\tau )^{8}+\vartheta _{{01}}(0;\tau )^{8}+\vartheta _{{10}}(0;\tau )^{8}\right]](/2014-wikipedia_en_all_02_2014/I/media/6/e/8/0/6e8020749144aacdf7fa2bea84dfdea3.png)
![\Delta (\tau )=16\pi ^{{12}}\left[\vartheta (0;\tau )\vartheta _{{01}}(0;\tau )\vartheta _{{10}}(0;\tau )\right]^{8}](/2014-wikipedia_en_all_02_2014/I/media/5/5/8/7/55872e469e22743838ccd6ccade07be5.png)
![j(\tau )=32{[\vartheta (0;\tau )^{8}+\vartheta _{{01}}(0;\tau )^{8}+\vartheta _{{10}}(0;\tau )^{8}]^{3} \over [\vartheta (0;\tau )\vartheta _{{01}}(0;\tau )\vartheta _{{10}}(0;\tau )]^{8}}](/2014-wikipedia_en_all_02_2014/I/media/d/5/9/7/d597141ba17e88df02a751aab1d41018.png)
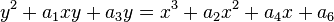

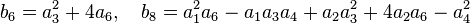
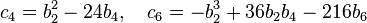
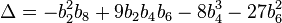


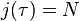
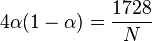
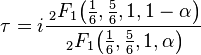
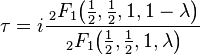
![{\begin{aligned}j\left(i\right)&=j\left({\tfrac {1+i}{2}}\right)=1\\j\left({\sqrt {2}}i\right)&=\left({\tfrac {5}{3}}\right)^{3}\\j\left(2i\right)&=\left({\tfrac {11}{2}}\right)^{3}\\j\left(2{\sqrt {2}}i\right)&=\left({\tfrac {5}{6}}\left[19+13{\sqrt {2}}\right]\right)^{3}\\j\left(4i\right)&=\left({\tfrac {1}{4}}\left[724+513{\sqrt {2}}\right]\right)^{3}\\j\left({\tfrac {1+2i}{2}}\right)&=\left({\tfrac {1}{4}}\left[724-513{\sqrt {2}}\right]\right)^{3}\\j\left({\tfrac {1+2{\sqrt {2}}i}{3}}\right)&=\left({\tfrac {5}{6}}\left[19-13{\sqrt {2}}\right]\right)^{3}\\j\left(3i\right)&=\left(2+{\sqrt {3}}\right)^{2}\left({\tfrac {1}{3}}\left[21+20{\sqrt {3}}\right]\right)^{3}\\j\left(2{\sqrt {3}}i\right)&={\tfrac {125}{16}}\left(30+17{\sqrt {3}}\right)^{3}\\j\left({\tfrac {1+7{\sqrt {3}}i}{2}}\right)&=-{\tfrac {1}{7}}\left(40\left[651+142{\sqrt {21}}\right]\right)^{3}\\j\left({\tfrac {1+3{\sqrt {11}}i}{10}}\right)&={\tfrac {64}{27}}\left(23-4{\sqrt {33}}\right)^{2}\left(-77+15{\sqrt {33}}\right)^{3}\\j\left({\sqrt {21}}i\right)&=\left({\tfrac {1}{2}}\left[5+3{\sqrt {3}}\right]\left[3+{\sqrt {7}}\right]\right)^{2}\left({\tfrac {1}{2}}\left[65+34{\sqrt {3}}+26{\sqrt {7}}+15{\sqrt {21}}\right]\right)^{3}\\j\left({\tfrac {{\sqrt {30}}i}{1}}\right)&=\left({\tfrac {1}{2}}\left[10+7{\sqrt {2}}+4{\sqrt {5}}+3{\sqrt {10}}\right]\right)^{4}\left(55+30{\sqrt {2}}+12{\sqrt {5}}+10{\sqrt {10}}\right)^{3}\\j\left({\tfrac {{\sqrt {30}}i}{2}}\right)&=\left({\tfrac {1}{2}}\left[10+7{\sqrt {2}}-4{\sqrt {5}}-3{\sqrt {10}}\right]\right)^{4}\left(55+30{\sqrt {2}}-12{\sqrt {5}}-10{\sqrt {10}}\right)^{3}\\j\left({\tfrac {{\sqrt {30}}i}{5}}\right)&=\left({\tfrac {1}{2}}\left[10-7{\sqrt {2}}+4{\sqrt {5}}-3{\sqrt {10}}\right]\right)^{4}\left(55-30{\sqrt {2}}+12{\sqrt {5}}-10{\sqrt {10}}\right)^{3}\\j\left({\tfrac {{\sqrt {30}}i}{10}}\right)&=\left({\tfrac {1}{2}}\left[10-7{\sqrt {2}}-4{\sqrt {5}}+3{\sqrt {10}}\right]\right)^{4}\left(55-30{\sqrt {2}}-12{\sqrt {5}}+10{\sqrt {10}}\right)^{3}\\j({\sqrt {70}}i)&=\left(1+{\tfrac {9}{4}}\left(303+220{\sqrt {2}}+139{\sqrt {5}}+96{\sqrt {10}}\right)^{2}\right)^{3}\\j(7i)&=\left(1+{\tfrac {9}{4}}{\sqrt {21+8{\sqrt {7}}}}\left(30+11{\sqrt {7}}+(6+{\sqrt {7}}){\sqrt {21+8{\sqrt {7}}}}\right)^{2}\right)^{3}\\j(8i)&=\left(1+{\tfrac {9}{4}}(1+{\sqrt {2}}){\sqrt {{\sqrt {2}}}}\left(123+104{\sqrt {{\sqrt {2}}}}+88{\sqrt {2}}+73{\sqrt {2}}{\sqrt {{\sqrt {2}}}}\right)^{2}\right)^{3}\\j\left({\tfrac {1+{\sqrt {1435}}i}{2}}\right)&=\left(1-9\left[9892538+4424079{\sqrt {5}}+1544955{\sqrt {41}}+690925{\sqrt {205}}\right]^{2}\right)^{3}\\j\left({\tfrac {1+{\sqrt {1555}}i}{2}}\right)&=\left(1-9\left[22297077+9971556{\sqrt {5}}+(3571365+1597163{\sqrt {5}}){\sqrt {{\tfrac {31+21{\sqrt {5}}}{2}}}}\right]^{2}\right)^{3}\end{aligned}}](/2014-wikipedia_en_all_02_2014/I/media/e/8/9/0/e8903fcc0e874aaebfe5caedf8d8c290.png)