Inversion (discrete mathematics)

From Wikipedia, the free encyclopedia

The permutation (4,1,5,2,6,3) has the inversion vector (0,1,0,2,0,3) and the inversion set {(1,2),(1,4),(3,4),(1,6),(3,6),(5,6)}. The inversion vector converted to decimal is 373.

Inversion set of the permutation
(0,15, 14,1, 13,2, 3,12,
11,4, 5,10, 6,9, 8,7)
showing the pattern of the
Thue–Morse sequence

In computer science and discrete mathematics, an inversion is a pair of places of a sequence where the elements on these places are out of their natural order.

Definitions

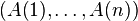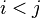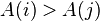Formally, let $(A(1),\ldots ,A(n))$ be a sequence of n distinct numbers. If $i<j$ and $A(i)>A(j)$ , then the pair 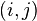$(i,j)$ is called an inversion of $A$ .^[1]^[2]

The inversion number of a sequence is one common measure of its sortedness.^[3]^[2] Formally, the inversion number is defined to be the number of inversions, that is,

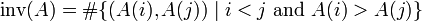${\text{inv}}(A)=\#\{(A(i),A(j))\mid i<j{\text{ and }}A(i)>A(j)\}$ .^[3]

Other measures of (pre-)sortedness include the minimum number of elements that can be deleted from the sequence to yield a fully sorted sequence, the number and lengths of sorted "runs" within the sequence, and the smallest number of exchanges needed to sort the sequence.^[4] Standard comparison sorting algorithms can be adapted to compute the inversion number in time $O(n log n)$ .

The inversion vector V(i) of the sequence is defined for i = 2, ..., n as $V[i]=\left\vert \{k\mid k<i{\text{ and }}A(k)>A(i)\}\right\vert$ . In other words each element is the number of elements preceding the element in the original sequence that are greater than it. Note that the inversion vector of a sequence has one less element than the sequence, because of course the number of preceding elements that are greater than the first is always zero. Each permutation of a sequence has a unique inversion vector and it is possible to construct any given permutation of a (fully sorted) sequence from that sequence and the permutation's inversion vector.^[5]

Weak order of permutations

The set of permutations on n items can be given the structure of a partial order, called the weak order of permutations, which forms a lattice.

To define this order, consider the items being permuted to be the integers from 1 to n, and let Inv(u) denote the set of inversions of a permutation u for the natural ordering on these items. That is, Inv(u) is the set of ordered pairs (i, j) such that 1 ≤ i < j ≤ n and u(i) > u(j). Then, in the weak order, we define u ≤ v whenever Inv(u) ⊆ Inv(v).

The edges of the Hasse diagram of the weak order are given by permutations u and v such that u < v and such that v is obtained from u by interchanging two consecutive values of u. These edges form a Cayley graph for the group of permutations that is isomorphic to the skeleton of a permutohedron.

The identity permutation is the minimum element of the weak order, and the permutation formed by reversing the identity is the maximum element.

References

↑ Cormen et al. 2001, pp. 39.
↑ 2.0 2.1 Vitter & Flajolet 1990, pp. 459.
↑ 3.0 3.1 Barth & Mutzel 2004, pp. 183.
↑ Mahmoud 2000, pp. 284.
↑ Pemmaraju & Skiena 2003, pp. 69.

Source bibliography

Barth, Wilhelm; Mutzel, Petra (2004). "Simple and Efficient Bilayer Cross Counting". Journal of Graph Algorithms and Applications 8 (2): 179–194.
Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001). Introduction to Algorithms (2nd ed.). MIT Press and McGraw-Hill. ISBN 0-262-53196-8.
Mahmoud, Hosam Mahmoud (2000). "Sorting Nonrandom Data". Sorting: a distribution theory. Wiley-Interscience series in discrete mathematics and optimization 54. Wiley-IEEE. ISBN 978-0-471-32710-3.
Pemmaraju, Sriram V.; Skiena, Steven S. (2003). "Permutations and combinations". Computational discrete mathematics: combinatorics and graph theory with Mathematica. Cambridge University Press. ISBN 978-0-521-80686-2.
Vitter, J.S.; Flajolet, Ph. (1990). "Average-Case Analysis of Algorithms and Data Structures". In van Leeuwen, Jan. Algorithms and Complexity 1 (2nd ed.). Elsevier. ISBN 978-0-444-88071-0.

Presortedness measures

Mannila, Heikki (1984). "Measures of presortedness and optimal sorting algorithms". Lecture Notes in Computer Science 172: 324–336. doi:10.1007/3-540-13345-3_29.
Estivill-Castro, Vladimir; Wood, Derick (1989). "A new measure of presortedness". Information and Computation 83 (1): 111–119.
Skiena, Steven S. (1988). "Encroaching lists as a measure of presortedness". BIT 28 (4): 755–784.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.