Interval order
In mathematics, especially order theory,
the interval order for a collection of intervals on the real line
is the partial order corresponding to their left-to-right precedence relation—one interval, I1, being considered less than another, I2, if I1 is completely to the left of I2.
More formally, a poset  is an interval order if and only if
there exists a bijection from
is an interval order if and only if
there exists a bijection from  to a set of real intervals,
so
to a set of real intervals,
so 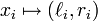 ,
such that for any
,
such that for any  we have
we have
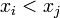 in
in  exactly when
exactly when 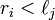 .
.
An interval order defined by unit intervals is a semiorder.
The complement of the comparability graph of an interval order ( , ≤)
is the interval graph
, ≤)
is the interval graph 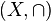 .
.
Interval orders should not be confused with the interval-containment orders, which are the containment orders on intervals on the real line (equivalently, the orders of dimension ≤ 2).
Interval dimension
The interval dimension of a partial order can be defined as the minimal number of interval order extensions realizing this order, in a similar way to the definition of the order dimension which uses linear extensions. The interval dimension of an order is always less than its order dimension,[1] but interval orders with high dimensions are known to exist. While the problem of determining the order dimension of general partial orders is known to be NP-complete, the complexity of determining the order dimension of an interval order is unknown.[2]
References
- Fishburn, Peter (1985). Interval Orders and Interval Graphs: A Study of Partially Ordered Sets. John Wiley.
- Gunther Schmidt, 2010. Relational Mathematics. Cambridge University Press, ISBN 978-0-521-76268-7.
- ↑ http://page.math.tu-berlin.de/~felsner/Paper/Idim-dim.pdf p.2
- ↑ http://page.math.tu-berlin.de/~felsner/Paper/diss.pdf, p.47