Intersection theorem

From Wikipedia, the free encyclopedia

In projective geometry, an intersection theorem or incidence theorem is an incidence structure consisting of points, lines, and possibly higher-dimensional objects and their incidences, together with a pair of nonincident objects A and B (for instance, a point and a line). The "theorem" states that, whenever a set of objects satisfies the incidences (i.e. can be matched up with the objects of the incidence structure in a way that preserves incidence), then objects determined by A and B must also be incident. An intersection theorem is not necessarily true in all projective geometries; it is rather a property which some geometries satisfy but not others.

For example, Desargues' theorem can be stated using the following incidence structure:

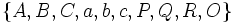
Points: $\{A,B,C,a,b,c,P,Q,R,O\}$
Lines: $\{AB,AC,BC,ab,ac,bc,Aa,Bb,Cc,PQ\}$
Incidences (in addition to obvious ones such as $(A,AB)$ : $\{(O,Aa),(O,Bb),(O,Cc),(P,BC),(P,bc),(Q,AC),(Q,ac),(R,AB),(R,ab)\}$

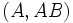The implication is then 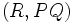$(R,PQ)$ —that point R is incident with line PQ.

Famous examples

Desargues' theorem holds in a projective plane P if and only if P is the projective plane over some division ring D— $P={\mathbb {P}}_{{2}}D$ . The projective plane is then called desarguesian. A theorem of Amitsur and Bergman states that, in the context of desarguesian projective planes, for every intersection theorem there is a rational identity such that the plane P satisfies the intersection theorem if and only if the division ring D satisfies the rational identity.

Pappus's hexagon theorem holds in a desarguesian projective plane ${\mathbb {P}}_{{2}}D$ if and only if D is a field; it corresponds to the identity $\forall a,b\in D,a\cdot b=b\cdot a$ .
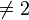Fano's theorem (which states a certain intersection does not happen) holds in ${\mathbb {P}}_{{2}}D$ if and only if D has characteristic $\neq 2$ ; it corresponds to the identity a+a=0.

References

L. H. Rowen; Polynomial Identities in Ring Theory. Academic Press: New York, 1980.
S. A. Amitsur; "Rational Identities and Applications to Algebra and Geometry", Journal of Algebra 3 no. 3 (1966), 304–359.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.