Intensity (physics)
In physics, intensity is the power transferred per unit area. In the SI system, it has units watts per metre squared (W/m2). It is used most frequently with waves (e.g. sound or light), in which case the average power transfer over one period of the wave is used. Intensity can be applied to other circumstances where energy is transferred. For example, one could calculate the intensity of the kinetic energy carried by drops of water from a garden sprinkler.
The word "intensity" as used here is not synonymous with "strength", "amplitude", "magnitude", or "level", as it sometimes is in colloquial speech.
Intensity can be found by taking the energy density (energy per unit volume) at a point in space and multiplying it by the velocity at which the energy is moving. The resulting vector has the units of power divided by area.
Mathematical description
If a point source is radiating energy in three dimensions and there is no energy lost to the medium, then the intensity decreases in proportion to distance from the object squared. This is an example of the inverse-square law.
Applying the law of conservation of energy, if the net power emanating is constant,
 ,
,
where P is the net power radiated, I is the intensity as a function of position, and dA is a differential element of a closed surface that contains the source.
If one integrates over a surface of uniform intensity I, for instance over a sphere centered around a point source radiating equally in all directions, the equation becomes
 ,
,
where I is the intensity at the surface of the sphere, and r is the radius of the sphere. ( is the expression for the surface area of a sphere).
is the expression for the surface area of a sphere).
Solving for I gives
 .
.
If the medium is damped, then the intensity drops off more quickly than the above equation suggests.
Anything that can transmit energy can have an intensity associated with it. For an electromagnetic wave, if E is the complex amplitude of the electric field, then the time-averaged energy density of the wave is given by
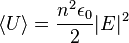 ,
,
and the intensity is obtained by multiplying this expression by the velocity of the wave, 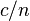 :
:
 ,
,
where n is the refractive index,  is the speed of light in vacuum and
is the speed of light in vacuum and  is the vacuum permittivity.
is the vacuum permittivity.
The treatment above does not hold for electromagnetic fields that are not radiating, such as for an evanescent wave. In these cases, the intensity can be defined as the magnitude of the Poynting vector.[1]
Alternative definitions of "intensity"
In photometry and radiometry intensity has a different meaning: it is the luminous or radiant power per unit solid angle. This can cause confusion in optics, where intensity can mean any of radiant intensity, luminous intensity or irradiance, depending on the background of the person using the term. Radiance is also sometimes called intensity, especially by astronomers and astrophysicists, and in heat transfer.
See also
| Quantity | Unit | Dimension | Notes | |||||
|---|---|---|---|---|---|---|---|---|
| Name | Symbol[nb 1] | Name | Symbol | Symbol | ||||
| Luminous energy | Qv [nb 2] | lumen second | lm⋅s | T⋅J [nb 3] | units are sometimes called talbots | |||
| Luminous flux | Φv [nb 2] | lumen (= cd⋅sr) | lm | J [nb 3] | also called luminous power | |||
| Luminous intensity | Iv | candela (= lm/sr) | cd | J [nb 3] | an SI base unit, luminous flux per unit solid angle | |||
| Luminance | Lv | candela per square metre | cd/m2 | L−2⋅J | units are sometimes called nits | |||
| Illuminance | Ev | lux (= lm/m2) | lx | L−2⋅J | used for light incident on a surface | |||
| Luminous emittance | Mv | lux (= lm/m2) | lx | L−2⋅J | used for light emitted from a surface | |||
| Luminous exposure | Hv | lux second | lx⋅s | L−2⋅T⋅J | ||||
| Luminous energy density | ωv | lumen second per metre3 | lm⋅s⋅m−3 | L−3⋅T⋅J | ||||
| Luminous efficacy | η [nb 2] | lumen per watt | lm/W | M−1⋅L−2⋅T3⋅J | ratio of luminous flux to radiant flux | |||
| Luminous efficiency | V | 1 | also called luminous coefficient | |||||
| See also: SI · Photometry · Radiometry · (Compare) | ||||||||
- ↑ Standards organizations recommend that photometric quantities be denoted with a suffix "v" (for "visual") to avoid confusion with radiometric or photon quantities. For example: USA Standard Letter Symbols for Illuminating Engineering USAS Z7.1-1967, Y10.18-1967
- ↑ 2.0 2.1 2.2 Alternative symbols sometimes seen: W for luminous energy, P or F for luminous flux, and ρ or K for luminous efficacy.
- ↑ 3.0 3.1 3.2 "J" here is the symbol for the dimension of luminous intensity, not the symbol for the unit joules.
| Quantity | Unit | Dimension | Notes | |||||
|---|---|---|---|---|---|---|---|---|
| Name | Symbol[nb 1] | Name | Symbol | Symbol | ||||
| Radiant energy | Qe[nb 2] | joule | J | M⋅L2⋅T−2 | energy | |||
| Radiant flux | Φe[nb 2] | watt | W or J/s | M⋅L2⋅T−3 | radiant energy per unit time, also called radiant power. | |||
| Spectral power | Φeλ[nb 2][nb 3] | watt per metre | W⋅m−1 | M⋅L⋅T−3 | radiant power per wavelength. | |||
| Radiant intensity | Ie | watt per steradian | W⋅sr−1 | M⋅L2⋅T−3 | power per unit solid angle. | |||
| Spectral intensity | Ieλ[nb 3] | watt per steradian per metre | W⋅sr−1⋅m−1 | M⋅L⋅T−3 | radiant intensity per wavelength. | |||
| Radiance | Le | watt per steradian per square metre | W⋅sr−1⋅m−2 | M⋅T−3 | power per unit solid angle per unit projected source area. confusingly called "intensity" in some other fields of study. | |||
| Spectral radiance | Leλ[nb 3] or Leν[nb 4] |
watt per steradian per metre3 or watt per steradian per square |
W⋅sr−1⋅m−3 or W⋅sr−1⋅m−2⋅Hz−1 |
M⋅L−1⋅T−3 or M⋅T−2 |
commonly measured in W⋅sr−1⋅m−2⋅nm−1 with surface area and either wavelength or frequency. | |||
| Irradiance | Ee[nb 2] | watt per square metre | W⋅m−2 | M⋅T−3 | power incident on a surface, also called radiant flux density. sometimes confusingly called "intensity" as well. | |||
| Spectral irradiance | Eeλ[nb 3] or Eeν[nb 4] |
watt per metre3 or watt per square metre per hertz |
W⋅m−3 or W⋅m−2⋅Hz−1 |
M⋅L−1⋅T−3 or M⋅T−2 |
commonly measured in W⋅m−2⋅nm−1 or 10−22 W⋅m−2⋅Hz−1, known as solar flux unit.[nb 5] | |||
| Radiant exitance / Radiant emittance |
Me[nb 2] | watt per square metre | W⋅m−2 | M⋅T−3 | power emitted from a surface. | |||
| Spectral radiant exitance / Spectral radiant emittance |
Meλ[nb 3] or Meν[nb 4] |
watt per metre3 or watt per square |
W⋅m−3 or W⋅m−2⋅Hz−1 |
M⋅L−1⋅T−3 or M⋅T−2 |
power emitted from a surface per unit wavelength or frequency. | |||
| Radiosity | Je | watt per square metre | W⋅m−2 | M⋅T−3 | emitted plus reflected power leaving a surface. | |||
| Spectral radiosity | Jeλ[nb 3] | watt per metre3 | W⋅m−3 | M⋅L−1⋅T−3 | emitted plus reflected power leaving a surface per unit wavelength | |||
| Radiant exposure | He | joule per square metre | J⋅m−2 | M⋅T−2 | also referred to as fluence | |||
| Radiant energy density | ωe | joule per metre3 | J⋅m−3 | M⋅L−1⋅T−2 | ||||
| See also: SI · Radiometry · Photometry · (Compare) | ||||||||
- ↑ Standards organizations recommend that radiometric quantities should be denoted with a suffix "e" (for "energetic") to avoid confusion with photometric or photon quantities.
- ↑ 2.0 2.1 2.2 2.3 2.4 Alternative symbols sometimes seen: W or E for radiant energy, P or F for radiant flux, I for irradiance, W for radiant emittance.
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 Spectral quantities given per unit wavelength are denoted with suffix "λ" (Greek) to indicate a spectral concentration. Spectral functions of wavelength are indicated by "(λ)" in parentheses instead, for example in spectral transmittance, reflectance and responsivity.
- ↑ 4.0 4.1 4.2 Spectral quantities given per unit frequency are denoted with suffix "ν" (Greek)—not to be confused with the suffix "v" (for "visual") indicating a photometric quantity.
- ↑ NOAA / Space Weather Prediction Center includes a definition of the solar flux unit (SFU).
References
- ↑ Paschotta, Rüdiger. "Optical Intensity". Encyclopedia of Laser Physics and Technology. RP Photonics.