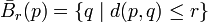Injective metric space
In metric geometry, an injective metric space, or equivalently a hyperconvex metric space, is a metric space with certain properties generalizing those of the real line and of L∞ distances in higher-dimensional vector spaces. These properties can be defined in two seemingly different ways: hyperconvexity involves the intersection properties of closed balls in the space, while injectivity involves the isometric embeddings of the space into larger spaces. However it is a theorem of Aronszajn and Panitchpakdi (1956; see e.g. Chepoi 1997) that these two different types of definitions are equivalent.
Hyperconvexity
A metric space X is said to be hyperconvex if it is convex and its closed balls have the binary Helly property. That is,
- any two points x and y can be connected by the isometric image of a line segment of length equal to the distance between the points (i.e. X is a path space), and
- if F is any family of closed balls
- such that each pair of balls in F meet, then there exists a point x common to all the balls in F.
Equivalently, if a set of points pi and radii ri > 0 satisfies ri + rj ≥ d(pi,pj) for each i and j, then there is a point q of the metric space that is within distance ri of each pi.
Injectivity
A retraction of a metric space X is a function ƒ mapping X to a subspace of itself, such that
- for all x, ƒ(ƒ(x)) = ƒ(x); that is, ƒ is the identity function on its image, and
- for all x and y, d(ƒ(x), ƒ(y)) ≤ d(x, y); that is, ƒ is nonexpansive.
A retract of a space X is a subspace of X that is an image of a retraction. A metric space X is said to be injective if, whenever X is isometric to a subspace Z of a space Y, that subspace Z is a retract of Y.
Examples
Examples of hyperconvex metric spaces include
- The real line
- Any vector space Rd with the L∞ distance
- Manhattan distance (L1) in the plane (which is equivalent up to rotation and scaling to the L∞), but not in higher dimensions
- The tight span of a metric space
- Any real tree
- Aim(X) – see Metric space aimed at its subspace
Due to the equivalence between hyperconvexity and injectivity, these spaces are all also injective.
Properties
In an injective space, the radius of the minimum ball that contains any set S is equal to half the diameter of S. This follows since the balls of radius half the diameter, centered at the points of S, intersect pairwise and therefore by hyperconvexity have a common intersection; a ball of radius half the diameter centered at a point of this common intersection contains all of S. Thus, injective spaces satisfy a particularly strong form of Jung's theorem.
Every injective space is a complete space (Aronszajn and Panitchpakdi 1956), and every metric map (or, equivalently, nonexpansive mapping, or short map) on a bounded injective space has a fixed point (Sine 1979; Soardi 1979). A metric space is injective if and only if it is an injective object in the category of metric spaces and metric maps. For additional properties of injective spaces see Espínola and Khamsi (2001).
References
- Aronszajn, N.; Panitchpakdi, P. (1956). "Extensions of uniformly continuous transformations and hyperconvex metric spaces". Pacific Journal of Mathematics 6: 405–439. MR 0084762. Correction (1957), Pacific J. Math. 7: 1729, MR 0092146.
- Chepoi, Victor (1997). "A TX approach to some results on cuts and metrics". Advances in Applied Mathematics 19 (4): 453–470. doi:10.1006/aama.1997.0549. MR 1479014.
- Espínola, R.; Khamsi, M. A. (2001). "Introduction to hyperconvex spaces". In Kirk, W. A.; Sims, B. (Eds.). Handbook of Metric Fixed Point Theory. Dordrecht: Kluwer Academic Publishers. MR 1904284.
- Isbell, J. R. (1964). "Six theorems about injective metric spaces". Commentarii Mathematici Helvetici 39: 65–76. doi:10.1007/BF02566944. MR 0182949.
- Sine, R. C. (1979). "On nonlinear contraction semigroups in sup norm spaces". Nonlinear Analysis 3 (6): 885–890. doi:10.1016/0362-546X(79)90055-5. MR 0548959.
- Soardi, P. (1979). "Existence of fixed points of nonexpansive mappings in certain Banach lattices". Proceedings of the American Mathematical Society 73 (1): 25–29. doi:10.2307/2042874. JSTOR 2042874. MR 0512051.