Ineffable cardinal
In the mathematics of transfinite numbers, an ineffable cardinal is a certain kind of large cardinal number, introduced by Jensen & Kunen (1969).
A cardinal number  is called almost ineffable if for every
is called almost ineffable if for every 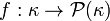 (where
(where 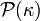 is the powerset of
is the powerset of  ) with the property that
) with the property that 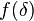 is a subset of
is a subset of  for all ordinals
for all ordinals 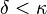 , there is a subset
, there is a subset 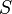 of
of  having cardinal
having cardinal  and homogeneous for
and homogeneous for  , in the sense that for any
, in the sense that for any  in
in 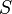 ,
,  .
.
A cardinal number  is called ineffable if for every binary-valued function
is called ineffable if for every binary-valued function  , there is a stationary subset of
, there is a stationary subset of  on which
on which  is homogeneous: that is, either
is homogeneous: that is, either  maps all unordered pairs of elements drawn from that subset to zero, or it maps all such unordered pairs to one.
maps all unordered pairs of elements drawn from that subset to zero, or it maps all such unordered pairs to one.
More generally,  is called
is called  -ineffable (for a positive integer
-ineffable (for a positive integer  ) if for every
) if for every 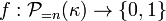 there is a stationary subset of
there is a stationary subset of  on which
on which  is
is  -homogeneous (takes the same value for all unordered
-homogeneous (takes the same value for all unordered  -tuples drawn from the subset). Thus, it is ineffable if and only if it is 2-ineffable.
-tuples drawn from the subset). Thus, it is ineffable if and only if it is 2-ineffable.
A totally ineffable cardinal is a cardinal that is  -ineffable for every
-ineffable for every 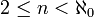 . If
. If  is
is 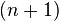 -ineffable, then the set of
-ineffable, then the set of  -ineffable cardinals below
-ineffable cardinals below  is a stationary subset of
is a stationary subset of  .
.
Totally ineffable cardinals are of greater consistency strength than subtle cardinals and of lesser consistency strength than remarkable cardinals. A list of large cardinal axioms by consistency strength is available here.
References
- Friedman, Harvey (2001), "Subtle cardinals and linear orderings", Annals of Pure and Applied Logic 107 (1–3): 1–34, doi:10.1016/S0168-0072(00)00019-1.
- Jensen, R. B.; Kunen, K. (1969), Some Combinatorial Properties of L and V, Unpublished manuscript