Indifference price
In finance, indifference pricing is a method of pricing financial securities with regard to a utility function. Also known as the reservation price or private valuation. Particularly the indifference price is the price that an agent would have the same expected utility level between exercising a financial transaction and not (with optimal trading otherwise). Typically the indifference price is a pricing range (a bid-ask spread) for a specific agent, this price range is an example of good-deal bounds.[1]
Mathematics
Given a utility function  and a claim
and a claim  with known payoffs at some terminal time
with known payoffs at some terminal time  . If we let the function
. If we let the function 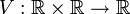 be defined by
be defined by
-
![V(x,k)=\sup _{{X_{T}\in {\mathcal {A}}(x)}}{\mathbb {E}}\left[u\left(X_{T}+kC_{T}\right)\right]](/2014-wikipedia_en_all_02_2014/I/media/a/0/5/8/a058dc7f9d608d4ddef94a14619f19a6.png) ,
,
where  is the initial endowment,
is the initial endowment,  is the set of all self-financing portfolios at time
is the set of all self-financing portfolios at time  starting with endowment
starting with endowment  , and
, and  is the number of the claim to be purchased (or sold). Then the indifference bid price
is the number of the claim to be purchased (or sold). Then the indifference bid price 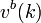 for
for  units of
units of  is the solution of
is the solution of 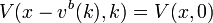 and the indifference ask price
and the indifference ask price 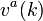 is the solution of
is the solution of 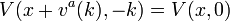 . The indifference price bound is the range
. The indifference price bound is the range ![\left[v^{b}(k),v^{a}(k)\right]](/2014-wikipedia_en_all_02_2014/I/media/3/4/0/8/3408c4ef75da8128b827af629372ce08.png) .[2]
.[2]
Example
Consider a market with a risk free asset  with
with 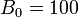 and
and  , and a risky asset
, and a risky asset 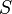 with
with 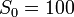 and
and  each with probability
each with probability 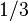 . Let your utility function be given by
. Let your utility function be given by 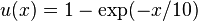 . To find either the bid or ask indifference price for a single European call option with strike 110, first calculate
. To find either the bid or ask indifference price for a single European call option with strike 110, first calculate 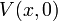 .
.
-
![V(x,0)=\max _{{\alpha B_{0}+\beta S_{0}=x}}{\mathbb {E}}[1-\exp(-.1\times (\alpha B_{T}+\beta S_{T}))]](/2014-wikipedia_en_all_02_2014/I/media/a/d/b/2/adb2cbd8a2a52141376ccd0142678d09.png)
-
![=\max _{{\beta }}\left[1-{\frac {1}{3}}\left[\exp \left(-{\frac {1.10x-20\beta }{10}}\right)+\exp \left(-{\frac {1.10x}{10}}\right)+\exp \left(-{\frac {1.10x+20\beta }{10}}\right)\right]\right]](/2014-wikipedia_en_all_02_2014/I/media/b/3/8/b/b38bd39d1675bc09d7cb77c23b7e553c.png) .
.
-
Which is maximized when  , therefore
, therefore 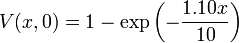 .
.
Now to find the indifference bid price solve for 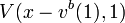
Which is maximized when  , therefore
, therefore ![V(x-v^{b}(1),1)=1-{\frac {1}{3}}\exp(-1.10x/10)\exp(1.10v^{b}(1)/10)\left[1+2\exp(-1)\right]](/2014-wikipedia_en_all_02_2014/I/media/b/3/0/8/b308d7775cee59426e61741c65a9815a.png) .
.
Therefore 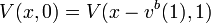 when
when 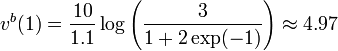 .
.
Similarly solve for 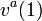 to find the indifference ask price.
to find the indifference ask price.
Notes
- If
![\left[v^{b}(k),v^{a}(k)\right]](/2014-wikipedia_en_all_02_2014/I/media/3/4/0/8/3408c4ef75da8128b827af629372ce08.png) are the indifference price bounds for a claim then by definition
are the indifference price bounds for a claim then by definition 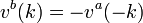 .[2]
.[2] - If
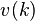 is the indifference bid price for a claim and
is the indifference bid price for a claim and  are the superhedging price and subhedging prices respectively then
are the superhedging price and subhedging prices respectively then  . Therefore, in a complete market the indifference price is always equal to the price to hedge the claim.
. Therefore, in a complete market the indifference price is always equal to the price to hedge the claim.
![V(x-v^{b}(1),1)=\max _{{\alpha B_{0}+\beta S_{0}=x-v^{b}(1)}}{\mathbb {E}}[1-\exp(-.1\times (\alpha B_{T}+\beta S_{T}+C_{T}))]](/2014-wikipedia_en_all_02_2014/I/media/a/1/c/8/a1c8a5fb5b7e0bdb35db215ce6fd3610.png)
![=\max _{{\beta }}\left[1-{\frac {1}{3}}\left[\exp \left(-{\frac {1.10(x-v^{b}(1))-20\beta }{10}}\right)+\exp \left(-{\frac {1.10(x-v^{b}(1))}{10}}\right)+\exp \left(-{\frac {1.10(x-v^{b}(1))+20\beta +20}{10}}\right)\right]\right]](/2014-wikipedia_en_all_02_2014/I/media/5/8/5/0/585092e28abfc835b2d2e717ab586f42.png)