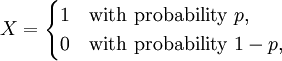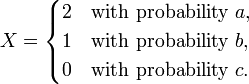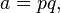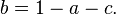Indecomposable distribution
From Wikipedia, the free encyclopedia
In probability theory, an indecomposable distribution is a probability distribution that cannot be represented as the distribution of the sum of two or more non-constant independent random variables: Z ≠ X + Y. If it can be so expressed, it is decomposable: Z = X + Y. If, further, it can be expressed as the distribution of the sum of two or more independent identically distributed random variables, then it is divisible: Z = X1 + X2.
Examples
Indecomposable
- The simplest examples are Bernoulli distributions: if
- then the probability distribution of X is indecomposable.
- Proof: Given non-constant distributions U and V, so that U assumes at least two values a, b and V assumes two values c, d, with a < b and c < d, then U + V assumes at least three distinct values: a + c, a + d, b + d (b + c may be equal to a + d, for example if one uses 0, 1 and 0, 1). Thus the sum of non-constant distributions assumes at least three values, so the Bernoulli distribution is not the sum of non-constant distributions.
- Suppose a + b + c = 1, a, b, c ≥ 0, and
- This probability distribution is decomposable (as the sum of two Bernoulli distributions) if
- and otherwise indecomposable. To see, this, suppose U and V are independent random variables and U + V has this probability distribution. Then we must have
- for some p, q ∈ [0, 1], by similar reasoning to the Bernoulli case (otherwise the sum U + V will assume more than three values). It follows that
- This system of two quadratic equations in two variables p and q has a solution (p, q) ∈ [0, 1]2 if and only if
- Thus, for example, the discrete uniform distribution on the set {0, 1, 2} is indecomposable, but the binomial distribution assigning respective probabilities 1/4, 1/2, 1/4 is decomposable.
- An absolutely continuous indecomposable distribution. It can be shown that the distribution whose density function is
- is indecomposable.
Decomposable
- All infinitely divisible distributions are a fortiori decomposable; in particular, this includes the stable distributions, such as the normal distribution.
- The uniform distribution on the interval [0, 1] is decomposable, since it is the sum of the Bernoulli variable that assumes 0 or 1/2 with equal probabilities and the uniform distribution on [0, 1/2]. Iterating this yields the infinite decomposition:
- where the independent random variables Xn are each equal to 0 or 1 with equal probabilities – this is a Bernoulli trial of each digit of the binary expansion.
- A sum of indecomposable random variables is necessarily decomposable (as it is a sum), and in fact may a fortiori be an infinitely divisible distribution (not just decomposable as the given sum). Suppose a random variable Y has a geometric distribution
- on {0, 1, 2, ...}. For any positive integer k, there is a sequence of negative-binomially distributed random variables Yj, j = 1, ..., k, such that Y1 + ... + Yk has this geometric distribution. Therefore, this distribution is infinitely divisible. But now let Dn be the nth binary digit of Y, for n ≥ 0. Then the Ds are independent and
- and each term in this sum is indecomposable.
Related concepts
At the other extreme from indecomposability is infinite divisibility.
- Cramér's theorem shows that while the normal distribution is infinitely divisible, it can only be decomposed into normal distributions.
- Cochran's theorem shows that decompositions of a sum of squares of normal random variables into sums of squares of linear combinations of these variables are always independent chi-squared distributions.
See also
References
- Lukacs, Eugene, Characteristic Functions, New York, Hafner Publishing Company, 1970.
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.