Impulse invariance
Impulse invariance is a technique for designing discrete-time infinite-impulse-response (IIR) filters from continuous-time filters in which the impulse response of the continuous-time system is sampled to produce the impulse response of the discrete-time system. The frequency response of the discrete-time system will be a sum of shifted copies of the frequency response of the continuous-time system; if the continuous-time system is approximately band-limited to a frequency less than the Nyquist frequency of the sampling, then the frequency response of the discrete-time system will be approximately equal to it for frequencies below the Nyquist frequency.
Discussion
The continuous-time system's impulse response, 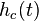 , is sampled with sampling period
, is sampled with sampling period  to produce the discrete-time system's impulse response,
to produce the discrete-time system's impulse response, ![h[n]](/2014-wikipedia_en_all_02_2014/I/media/7/6/d/f/76df30cb2f3c2675e057e25429917f27.png) .
.
Thus, the frequency responses of the two systems are related by
If the continuous time filter is approximately band-limited (i.e. 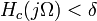 when
when  ), then the frequency response of the discrete-time system will be approximately the continuous-time system's frequency response for frequencies below π radians per sample (below the Nyquist frequency 1/(2T) Hz):
), then the frequency response of the discrete-time system will be approximately the continuous-time system's frequency response for frequencies below π radians per sample (below the Nyquist frequency 1/(2T) Hz):
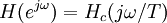 for
for 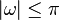
Comparison to the bilinear transform
Note that aliasing will occur, including aliasing below the Nyquist frequency to the extent that the continuous-time filter's response is nonzero above that frequency. The bilinear transform is an alternative to impulse invariance that uses a different mapping that maps the continuous-time system's frequency response, out to infinite frequency, into the range of frequencies up to the Nyquist frequency in the discrete-time case, as opposed to mapping frequencies linearly with circular overlap as impulse invariance does.
Effect on poles in system function
If the continuous poles at  , the system function can be written in partial fraction expansion as
, the system function can be written in partial fraction expansion as
Thus, using the inverse Laplace transform, the impulse response is
The corresponding discrete-time system's impulse response is then defined as the following
Performing a z-transform on the discrete-time impulse response produces the following discrete-time system function
Thus the poles from the continuous-time system function are translated to poles at z = eskT. The zeros, if any, are not so simply mapped.
Poles and zeros
If the system function has zeros as well as poles, they can be mapped the same way, but the result is no longer an impulse invariance result: the discrete-time impulse response is not equal simply to samples of the continuous-time impulse response. This method is known as the matched Z-transform method, or pole–zero mapping. In the case of all-pole filters, the methods are equivalent.
Stability and causality
Since poles in the continuous-time system at s = sk transform to poles in the discrete-time system at z = exp(skT), poles in the left half of the s-plane map to inside the unit circle in the z-plane; so if the continuous-time filter is causal and stable, then the discrete-time filter will be causal and stable as well.
Corrected formula
When a causal continuous-time impulse response has a discontinuity at 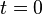 , the expressions above are not consistent.[1]
This is because
, the expressions above are not consistent.[1]
This is because  should really only contribute half its value to
should really only contribute half its value to ![h[0]](/2014-wikipedia_en_all_02_2014/I/media/d/0/c/e/d0ceb83e8678d99071dc1340f5f85647.png) .
.
Making this correction gives
Performing a z-transform on the discrete-time impulse response produces the following discrete-time system function
See also
- Infinite impulse response
- Bilinear transform
- Matched Z-transform method
- Continuous-time filters:
References
- ↑ L. Jackson, "A correction to impulse invariance", IEEE Signal Processing Letters, Vol. 7, Oct. 2000.
Other sources
- Oppenheim, Alan V. and Schafer, Ronald W. with Buck, John R. Discrete-Time Signal Processing. Second Edition. Upper Saddle River, New Jersey: Prentice-Hall, 1999.
- Sahai, Anant. Course Lecture. Electrical Engineering 123: Digital Signal Processing. University of California, Berkeley. 5 April 2007.
External links
- Impulse Invariant Transform at CircuitDesign.info Brief explanation, an example, and application to Continuous Time Sigma Delta ADC's.
| ||||||||||||||
![h[n]=Th_{c}(nT)\,](/2014-wikipedia_en_all_02_2014/I/media/2/1/2/c/212ca6fa54656801f4515bba1be6421b.png)
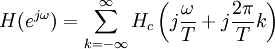
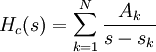
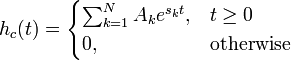
![h[n]=T\sum _{{k=1}}^{N}{A_{k}e^{{s_{k}nT}}u[n]}\,](/2014-wikipedia_en_all_02_2014/I/media/9/c/0/a/9c0a5a35716966914b1cac94ef44cb2a.png)
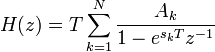
![h[n]=T\left(h_{c}(nT)-{\frac {1}{2}}h_{c}(0)\delta [n]\right)\,](/2014-wikipedia_en_all_02_2014/I/media/6/a/d/d/6add4d9c4a3fa603331963afdce50af8.png)
![h[n]=T\sum _{{k=1}}^{N}{A_{k}e^{{s_{k}nT}}}\left(u[n]-{\frac {1}{2}}\delta [n]\right)\,](/2014-wikipedia_en_all_02_2014/I/media/9/a/c/0/9ac0029f6985c345ce40319af657eba4.png)
