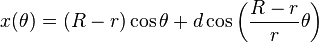Hypotrochoid
From Wikipedia, the free encyclopedia

The red curve is a hypotrochoid drawn as the smaller black circle rolls around inside the larger blue circle (parameters are R = 5, r = 3, d = 5).
A hypotrochoid is a roulette traced by a point attached to a circle of radius r rolling around the inside of a fixed circle of radius R, where the point is a distance d from the center of the interior circle.
The parametric equations for a hypotrochoid are:[citation needed]
Where 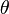 is the angle formed by the horizontal and the center of the rolling circle (note that these are not polar equations because
is the angle formed by the horizontal and the center of the rolling circle (note that these are not polar equations because 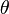 is not the polar angle).
is not the polar angle).
Special cases include the hypocycloid with d = r and the ellipse with R = 2r.

The ellipse (drawn in red) may be expressed as a special case of the hypotrochoid, with R = 2r; here R = 10, r = 5, d = 1.
The classic Spirograph toy traces out hypotrochoid and epitrochoid curves.
See also
References
- J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. pp. 165–168. ISBN 0-486-60288-5.
External links
- Flash Animation of Hypocycloid
- Hypotrochoid from Visual Dictionary of Special Plane Curves, Xah Lee
- Interactive hypotrochoide animation
- O'Connor, John J.; Robertson, Edmund F., "Hypotrochoid", MacTutor History of Mathematics archive, University of St Andrews.
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.