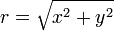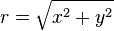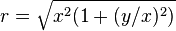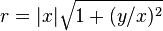Hypot

From Wikipedia, the free encyclopedia

Hypot is a mathematical function defined to calculate the length of the hypotenuse of a right-angle triangle. It was designed to avoid errors arising due to limited-precision calculations performed on computers.

Motivation and usage

Calculation of the length of the hypotenuse of a triangle is possible to do using the square root function but hypot(x, y) avoids possible problems with very large or very small numbers.

The magnitude of the hypotenuse from (0, 0) to (x, y) can be calculated using:

$r={\sqrt {x^{2}+y^{2}}}\,$

However the squares of very large or small values of x and y may exceed the range of machine precision when calculated on a computer, leading to an inaccurate result (see underflow, overflow). The hypot function was designed to calculate the result without causing this problem.

The hypot function may typically be used together with the atan2 function to convert from Cartesian to polar coordinates:

r = hypot(x, y) θ = atan2(y, x)

This operation is also known as Pythagorean addition.

Implementation

The difficulty with the naive implementation is that x² or y² may overflow or underflow, unless the intermediate result is computed with extended precision. A common implementation technique is to exchange the values, if necessary, so that |x| > |y|, and then use the equivalent form derived thusly:

$r={\sqrt {x^{2}+y^{2}}}$

$r={\sqrt {x^{2}(1+(y/x)^{2})}}$

$r=|x|{\sqrt {1+(y/x)^{2}}}$

The computation of y/x cannot overflow, and underflows compute the correct result. The square root is computed over a value between 1 and 2. Finally, the multiplication by |x| cannot underflow, and overflows only when the result is too large to represent.

Pseudocode:

double hypot(double x,double y)
{
    double t;
    x = abs(x);
    y = abs(y);
    t = min(x,y);
    x = max(x,y);
    t = t/x;
    return x*sqrt(1+t*t);
}

Programming language support

The function is present in several programming languages:

C99
C++11
Fortran 2008
Python
Apple's PowerPC Numerics ^[1]
MATLAB^[2]
Pascal ^[3]
PHP^[4]
Java (since version 1.5)^[5]
Ruby ^[6]
Go ^[7]
Rust ^[8]
Javascript ^[9]
Some C90 and C++ libraries have provided a hypot function.^[10]^[11]^[12]

References

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.

Hypot

Motivation and usage

Implementation

Programming language support

See also

References