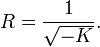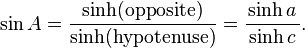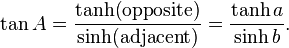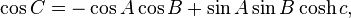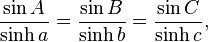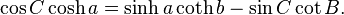Hyperbolic triangle

From Wikipedia, the free encyclopedia

Not to be confused with the hyperbolic triangle of a hyperbolic sector

In hyperbolic geometry, a hyperbolic triangle is a triangle in the hyperbolic plane. It consists of three line segments called sides or edges and three points called angles or vertices.

Just as in the Euclidean case, three points of a hyperbolic space of an arbitrary dimension always lie on the same plane. Hence planar hyperbolic triangles also describe triangles possible in any higher dimension of hyperbolic spaces.

A tiling of the hyperbolic plane with hyperbolic triangles – the order-7 triangular tiling.

Definition

A hyperbolic triangle consists of three non-collinear points and three segments between them.^[1] The relations among the angles and sides are analogous to those of spherical trigonometry; they are most conveniently stated if the lengths are measured in terms of a special unit of length analogous to a radian.^[2] In terms of the Gaussian curvature $K$ of the plane this unit is given by

$R={\frac {1}{{\sqrt {-K}}}}.$

In a hyperbolic triangle the sum of the angles A, B, C (respectively opposite to the side with the corresponding letter) is strictly less than a straight angle. This is contrasted to Euclidean triangles where this sum is always equal to the straight angle, as well as to spherical triangles where this sum is greater. The difference is often called the defect of the triangle. The area of a hyperbolic triangle is equal to its defect multiplied by the square of $R$ :

$(\pi -A-B-C)R^{2}{}{}.\!$

This theorem, first proven by Johann Heinrich Lambert,^[3] corresponds to Girard's theorem in spherical geometry. In all the formulas stated below the sides $a$ , $b$ , and $c$ must be measured in this unit. In other words, $R$ is supposed to be equal to 1.

Ideal vertices

Ideal triangles in infinite-order triangular tiling {3,∞}

The definition of a triangle can be generalized, permitting for vertices outside the plane itself, but keeping sides within the plane. If a pair of sides is asymptotic (i.e. distance between them vanishes but they do not intersect), then they end at an ideal vertex represented as an omega point. Such pair of sides may also be said to form an angle of zero. It is impossible in Euclidean geometry for straight sides lying on distinct lines. Though, such zero angles are common with tangent circles.

A triangle with one ideal vertex is called an omega triangle. If all three vertices are ideal, then the resulting figure is called an ideal triangle. The latter is characterized by zero sum of the angles.

Right triangles

Trigonometry formulas for hyperbolic triangles depend on the hyperbolic functions sinh, cosh, and tanh: If C is a right angle then:

The sine of angle A is the ratio of the hyperbolic sine of the side opposite the angle to the hyperbolic sine of the hypotenuse.

$\sin A={\frac {{\textrm {sinh(opposite)}}}{{\textrm {sinh(hypotenuse)}}}}={\frac {\sinh a}{\,\sinh c\,}}.\,$

The cosine of angle A is the ratio of the hyperbolic tangent of the adjacent leg to the hyperbolic tangent of the hypotenuse.

$\cos A={\frac {{\textrm {tanh(adjacent)}}}{{\textrm {tanh(hypotenuse)}}}}={\frac {\tanh b}{\,\tanh c\,}}.\,$

The tangent of angle A is the ratio of the hyperbolic tangent of the opposite leg to the hyperbolic sine of the adjacent leg.

$\tan A={\frac {{\textrm {tanh(opposite)}}}{{\textrm {sinh(adjacent)}}}}={\frac {\tanh a}{\,\sinh b\,}}.$

The instance of an ideal right triangle provides the configuration to examine the angle of parallelism in the triangle.

Oblique triangles

Whether C is a right angle or not, the following relationships hold: The hyperbolic law of cosines is as follows:

$\cosh c=\cosh a\cosh b-\sinh a\sinh b\cos C,$

Its dual is

$\cos C=-\cos A\cos B+\sin A\sin B\cosh c,$

There is also a law of sines:

${\frac {\sin A}{\sinh a}}={\frac {\sin B}{\sinh b}}={\frac {\sin C}{\sinh c}},$

and a four-parts formula:

$\cos C\cosh a=\sinh a\coth b-\sin C\cot B.$

References

↑ Stothers, Wilson (2000), Hyperbolic geometry, University of Glasgow , interactive instructional website
↑ For instance, the absolute length scales for both spherical geometry (the radian) and hyperbolic geometry can be defined as the perimeters of equilateral triangles with fixed angular defects; see Needham, Tristan (1998), Visual Complex Analysis, Oxford University Press, p. 270, ISBN 9780198534464 . As with the radian, the choice of units for this length scale is the one that makes the area formula as simple as possible.
↑ Ratcliffe, John (2006), Foundations of Hyperbolic Manifolds, Graduate Texts in Mathematics 149, Springer, p. 99, ISBN 9780387331973, "That the area of a hyperbolic triangle is proportional to its angle defect first appeared in Lambert's monograph Theorie der Parallellinien, which was published posthumously in 1786."