Hydrostatic stress
In continuum mechanics, a hydrostatic stress is an isotropic stress that is given by the weight of water above a certain point. It is often used interchangeably with "pressure" and is also known as confining stress, particularly in the field geomechanics. Its magnitude 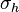 can be given by:
can be given by:
where  is an index denoting each distinct layer of material above the point of interest,
is an index denoting each distinct layer of material above the point of interest,  is the density of each layer,
is the density of each layer, 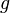 is the gravitational acceleration (assumed constant here; this can be substituted with any acceleration that is important in defining weight), and
is the gravitational acceleration (assumed constant here; this can be substituted with any acceleration that is important in defining weight), and  is the height (or thickness) of each given layer of material. For example, the magnitude of the hydrostatic stress felt at a point under ten meters of fresh water would be
is the height (or thickness) of each given layer of material. For example, the magnitude of the hydrostatic stress felt at a point under ten meters of fresh water would be
where the index  indicates "water".
indicates "water".
Because the hydrostatic stress is isotropic, it acts equally in all directions. In tensor form, the hydrostatic stress is equal to
where 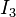 is the 3-by-3 identity matrix.
is the 3-by-3 identity matrix.

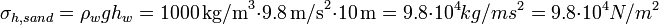
![\sigma _{h}\cdot I_{3}=\left[{\begin{array}{ccc}\sigma _{h}&0&0\\0&\sigma _{h}&0\\0&0&\sigma _{h}\end{array}}\right]](/2014-wikipedia_en_all_02_2014/I/media/8/2/0/b/820b6540cdd69f0031ae6185a900dbf7.png)