Hydrodynamic radius

From Wikipedia, the free encyclopedia

The hydrodynamic radius of a macromolecule or colloid particle has two meanings. Some books use it as a synonym for the Stokes radius. ^[1]

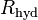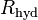Others books define a theoretical hydrodynamic radius $R_{{{\rm {hyd}}}}$ . They consider the macromolecule or colloid particle to be a collection of $N$ subparticles. This is done most commonly for polymers; the subparticles would then be the units of the polymer. $R_{{{\rm {hyd}}}}$ is defined by

${\frac {1}{R_{{{\rm {hyd}}}}}}\ {\stackrel {{\mathrm {def}}}{=}}\ {\frac {1}{N^{{2}}}}\left\langle \sum _{{i\neq j}}{\frac {1}{r_{{ij}}}}\right\rangle$

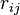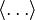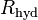where $r_{{ij}}$ is the distance between subparticles $i$ and $j$ , and where the angular brackets $\langle \ldots \rangle$ represent an ensemble average. ^[2] The theoretical hydrodynamic radius $R_{{{\rm {hyd}}}}$ was originally an estimate by John Gamble Kirkwood of the Stokes radius of a polymer.

The theoretical hydrodynamic radius 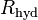$R_{{{\rm {hyd}}}}$ arises in the study of the dynamic properties of polymers moving in a solvent. It is often similar in magnitude to the radius of gyration.

Notes

↑ Gert R. Strobl (1996). The Physics of Polymers Concepts for Understanding Their Structures and Behavior. Springer-Verlag. ISBN 3-540-60768-4. Section 6.4 page 290.
↑ J. Des Cloizeaux and G. Jannink (1990). Polymers in Solution Their Modelling and Structure. Clarendon Press. ISBN 0-19-852036-0. Chapter 10, Section 7.4, pages 415-417.

References

Grosberg AY and Khokhlov AR. (1994) Statistical Physics of Macromolecules (translated by Atanov YA), AIP Press. ISBN 1-56396-071-0

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.