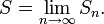Hutchinson operator

From Wikipedia, the free encyclopedia

In mathematics, in the study of fractals, a Hutchinson operator (also known as the Barnsley Operator[1]) is a collection of functions on an underlying space E. The iteration of these functions gives rise to the attractor of an iterated function system, for which the fixed set is self-similar.

Definition

Formally, let 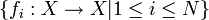\{f_{i}:X\to X|1\leq i\leq N\} be an iterated function system, or a set of N contractions from a compact set X to itself. We may regard this as defining an operator H on the power set P X as

H:A\mapsto \bigcup _{{i=1}}^{N}f_{i}[A],\,

where A is any subset of X.

A key question in the theory is to describe the fixed sets of the operator H. One way of constructing such a fixed set is to start with an initial point or set S0 and iterate the actions of the fi, taking Sn+1 to be the union of the images of Sn under the operator H; then taking S to be the union of the Sn, that is,

S_{{n+1}}=\bigcup _{{i=1}}^{N}f_{i}[S_{n}]

and

S=\lim _{{n\to \infty }}S_{n}.

Properties

Hutchinson (1981) considered the case when the fi are contraction mappings on a Euclidean space X = Rd. He showed that such a system of functions has a unique compact (closed and bounded) fixed set S. The proof[2] consists in showing that the Hutchinson operator itself is a contraction mapping on the set of compact subsets of X (endowed with the Hausdorff distance).

The collection of functions f_{i} together with composition form a monoid. With N functions, then one may visualize the monoid as a full N-ary tree or a Cayley tree.

See also

Notes

  1. ↑ Parallel Processing and Applied Mathematics: 7th International Conference ... By Roman Wyrzykowski
  2. ↑ Sagan, Hans (1994). Space filling curves. New York ;Berlin [u.a.]: Springer. ISBN 0-387-94265-3. 

References

  • Hutchinson, John E. (1981). "Fractals and self similarity". Indiana Univ. Math. J. 30 (5): 713–747. doi:10.1512/iumj.1981.30.30055. 
  • Heinz-Otto Peitgen; Hartmut Jürgens, Dietmar Saupe (2004). Chaos and Fractals: New Frontiers of Science. Springer-Verlag. pp. 84,225. ISBN 0-387-20229-3. 
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.