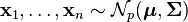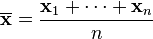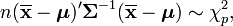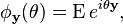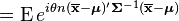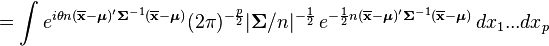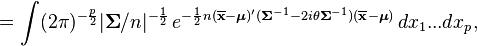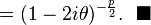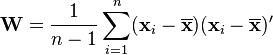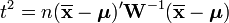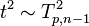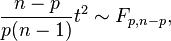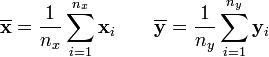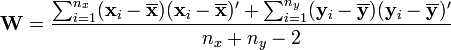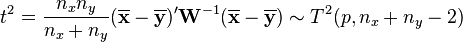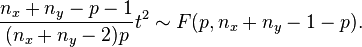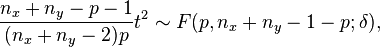Hotelling's T-squared distribution

From Wikipedia, the free encyclopedia

In statistics Hotelling's T-squared distribution is a univariate distribution proportional to the F-distribution and arises importantly as the distribution of a set of statistics which are natural generalizations of the statistics underlying Student's t-distribution. In particular, the distribution arises in multivariate statistics in undertaking tests of the differences between the (multivariate) means of different populations, where tests for univariate problems would make use of a t-test.

The distribution is named for Harold Hotelling, who developed it^[1] as a generalization of Student's t-distribution.

The distribution

If the vector _pd₁ is Gaussian multivariate-distributed with zero mean and unit covariance matrix N(_p0₁,_pI_p) and _mM_p is a p x p matrix with a Wishart distribution with unit scale matrix and m degrees of freedom W(_pI_p,m) then m(₁d' _pM⁻¹_pd₁) has a Hotelling T² distribution with dimensionality parameter p and m degrees of freedom.^[2]

If the notation 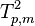$T_{{p,m}}^{2}$ is used to denote a random variable having Hotelling's T-squared distribution with parameters p and m then, if a random variable X has Hotelling's T-squared distribution,

$X\sim T_{{p,m}}^{2}$

then^[1]

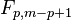${\frac {m-p+1}{pm}}X\sim F_{{p,m-p+1}}$

where $F_{{p,m-p+1}}$ is the F-distribution with parameters p and m−p+1.

Hotelling's T-squared statistic

Hotelling's T-squared statistic is a generalization of Student's t statistic that is used in multivariate hypothesis testing, and is defined as follows.^[1]

Let 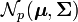${\mathcal {N}}_{p}({\boldsymbol {\mu }},{{\mathbf \Sigma }})$ denote a p-variate normal distribution with location 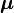${\boldsymbol {\mu }}$ and covariance ${{\mathbf \Sigma }}$ . Let

${{\mathbf x}}_{1},\dots ,{{\mathbf x}}_{n}\sim {\mathcal {N}}_{p}({\boldsymbol {\mu }},{{\mathbf \Sigma }})$

be n independent random variables, which may be represented as 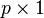$p\times 1$ column vectors of real numbers. Define

$\overline {{\mathbf x}}={\frac {{\mathbf {x}}_{1}+\cdots +{\mathbf {x}}_{n}}{n}}$

to be the sample mean. It can be shown that

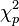$n(\overline {{\mathbf x}}-{\boldsymbol {\mu }})'{{\mathbf \Sigma }}^{{-1}}(\overline {{\mathbf x}}-{\boldsymbol {{\mathbf \mu }}})\sim \chi _{p}^{2},$

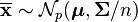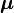where $\chi _{p}^{2}$ is the chi-squared distribution with p degrees of freedom. To show this use the fact that $\overline {{\mathbf x}}\sim {\mathcal {N}}_{p}({\boldsymbol {\mu }},{{\mathbf \Sigma }}/n)$ and then derive the characteristic function of the random variable ${\mathbf y}=n(\overline {{\mathbf x}}-{\boldsymbol {\mu }})'{{\mathbf \Sigma }}^{{-1}}(\overline {{\mathbf x}}-{\boldsymbol {{\mathbf \mu }}})$ . This is done below,

$\phi _{{{\mathbf y}}}(\theta )=\operatorname {E}e^{{i\theta {\mathbf y}}},$

$=\operatorname {E}e^{{i\theta n(\overline {{\mathbf x}}-{\boldsymbol {\mu }})'{{\mathbf \Sigma }}^{{-1}}(\overline {{\mathbf x}}-{\boldsymbol {{\mathbf \mu }}})}}$

$=\int e^{{i\theta n(\overline {{\mathbf x}}-{\boldsymbol {\mu }})'{{\mathbf \Sigma }}^{{-1}}(\overline {{\mathbf x}}-{\boldsymbol {{\mathbf \mu }}})}}(2\pi )^{{-{\frac {p}{2}}}}|{\boldsymbol \Sigma }/n|^{{-{\frac {1}{2}}}}\,e^{{-{\frac {1}{2}}n(\overline {{\mathbf x}}-{\boldsymbol \mu })'{\boldsymbol \Sigma }^{{-1}}(\overline {{\mathbf x}}-{\boldsymbol \mu })}}\,dx_{{1}}...dx_{{p}}$

$=\int (2\pi )^{{-{\frac {p}{2}}}}|{\boldsymbol \Sigma }/n|^{{-{\frac {1}{2}}}}\,e^{{-{\frac {1}{2}}n(\overline {{\mathbf x}}-{\boldsymbol \mu })'({\boldsymbol \Sigma }^{{-1}}-2i\theta {\boldsymbol \Sigma }^{{-1}})(\overline {{\mathbf x}}-{\boldsymbol \mu })}}\,dx_{{1}}...dx_{{p}},$

$=|({\boldsymbol \Sigma }^{{-1}}-2i\theta {\boldsymbol \Sigma }^{{-1}})^{{-1}}/n|^{{{\frac {1}{2}}}}|{\boldsymbol \Sigma }/n|^{{-{\frac {1}{2}}}}\int (2\pi )^{{-{\frac {p}{2}}}}|({\boldsymbol \Sigma }^{{-1}}-2i\theta {\boldsymbol \Sigma }^{{-1}})^{{-1}}/n|^{{-{\frac {1}{2}}}}\,e^{{-{\frac {1}{2}}n(\overline {{\mathbf x}}-{\boldsymbol \mu })'({\boldsymbol \Sigma }^{{-1}}-2i\theta {\boldsymbol \Sigma }^{{-1}})(\overline {{\mathbf x}}-{\boldsymbol \mu })}}\,dx_{{1}}...dx_{{p}},$

$=|({\mathbf I}_{p}-2i\theta {\mathbf I}_{p})|^{{-{\frac {1}{2}}}},$

$=(1-2i\theta )^{{-{\frac {p}{2}}}}.~~\blacksquare$

However, ${{\mathbf \Sigma }}$ is often unknown and we wish to do hypothesis testing on the location ${\boldsymbol {\mu }}$ .

Sum of p squared t's

Define

${{\mathbf W}}={\frac {1}{n-1}}\sum _{{i=1}}^{n}({\mathbf {x}}_{i}-\overline {{\mathbf x}})({\mathbf {x}}_{i}-\overline {{\mathbf x}})'$

to be the sample covariance. Here we denote transpose by an apostrophe. It can be shown that 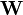${\mathbf W}$ is positive-definite and 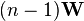$(n-1){\mathbf W}$ follows a p-variate Wishart distribution with n−1 degrees of freedom.^[3] Hotelling's T-squared statistic is then defined^[4] to be

$t^{2}=n(\overline {{\mathbf x}}-{\boldsymbol {\mu }})'{{\mathbf W}}^{{-1}}(\overline {{\mathbf x}}-{\boldsymbol {{\mathbf \mu }}})$

and, also from above,

$t^{2}\sim T_{{p,n-1}}^{2}$

i.e.

${\frac {n-p}{p(n-1)}}t^{2}\sim F_{{p,n-p}},$

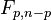where $F_{{p,n-p}}$ is the F-distribution with parameters p and n−p. In order to calculate a p value, multiply the t² statistic by the above constant and use the F-distribution.

Hotelling's two-sample T-squared statistic

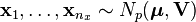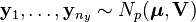If ${{\mathbf x}}_{1},\dots ,{{\mathbf x}}_{{n_{x}}}\sim N_{p}({\boldsymbol {\mu }},{{\mathbf V}})$ and ${{\mathbf y}}_{1},\dots ,{{\mathbf y}}_{{n_{y}}}\sim N_{p}({\boldsymbol {\mu }},{{\mathbf V}})$ , with the samples independently drawn from two independent multivariate normal distributions with the same mean and covariance, and we define

$\overline {{\mathbf x}}={\frac {1}{n_{x}}}\sum _{{i=1}}^{{n_{x}}}{\mathbf {x}}_{i}\qquad \overline {{\mathbf y}}={\frac {1}{n_{y}}}\sum _{{i=1}}^{{n_{y}}}{\mathbf {y}}_{i}$

as the sample means, and

${{\mathbf W}}={\frac {\sum _{{i=1}}^{{n_{x}}}({\mathbf {x}}_{i}-\overline {{\mathbf x}})({\mathbf {x}}_{i}-\overline {{\mathbf x}})'+\sum _{{i=1}}^{{n_{y}}}({\mathbf {y}}_{i}-\overline {{\mathbf y}})({\mathbf {y}}_{i}-\overline {{\mathbf y}})'}{n_{x}+n_{y}-2}}$

as the unbiased pooled covariance matrix estimate, then Hotelling's two-sample T-squared statistic is

$t^{2}={\frac {n_{x}n_{y}}{n_{x}+n_{y}}}(\overline {{\mathbf x}}-\overline {{\mathbf y}})'{{\mathbf W}}^{{-1}}(\overline {{\mathbf x}}-\overline {{\mathbf y}})\sim T^{2}(p,n_{x}+n_{y}-2)$

and it can be related to the F-distribution by^[3]

${\frac {n_{x}+n_{y}-p-1}{(n_{x}+n_{y}-2)p}}t^{2}\sim F(p,n_{x}+n_{y}-1-p).$

The non-null distribution of this statistic is the noncentral F-distribution (the ratio of a non-central Chi-squared random variable and an independent central Chi-squared random variable)

${\frac {n_{x}+n_{y}-p-1}{(n_{x}+n_{y}-2)p}}t^{2}\sim F(p,n_{x}+n_{y}-1-p;\delta ),$

with

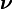$\delta ={\frac {n_{x}n_{y}}{n_{x}+n_{y}}}{\boldsymbol {\nu }}'{\mathbf {V}}^{{-1}}{\boldsymbol {\nu }},$

where ${\boldsymbol {\nu }}$ is the difference vector between the population means.

References

↑ 1.0 1.1 1.2 Hotelling, H. (1931). "The generalization of Student's ratio". Annals of Mathematical Statistics 2 (3): 360–378. doi:10.1214/aoms/1177732979.
↑ Eric W. Weisstein, CRC Concise Encyclopedia of Mathematics, Second Edition, Chapman & Hall/CRC, 2003, p. 1408
↑ 3.0 3.1 K.V. Mardia, J.T. Kent, and J.M. Bibby (1979) Multivariate Analysis, Academic Press.
↑ http://www.itl.nist.gov/div898/handbook/pmc/section5/pmc543.htm

External links

Prokhorov, A.V. (2001), "Hotelling T²-distribution", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4

Probability distributions

Discrete univariate with finite support

Benford Bernoulli Beta-binomial binomial categorical hypergeometric Poisson binomial Rademacher discrete uniform Zipf Zipf–Mandelbrot

Discrete univariate with infinite support

beta negative binomial Borel Conway–Maxwell–Poisson discrete phase-type Delaporte extended negative binomial Gauss–Kuzmin geometric logarithmic negative binomial parabolic fractal Poisson Skellam Yule–Simon zeta

Continuous univariate supported on a bounded interval, e.g. [0,1]

Arcsine ARGUS Balding–Nichols Bates Beta Beta rectangular Irwin–Hall Kumaraswamy logit-normal Noncentral beta raised cosine Triangular U-quadratic uniform Wigner semicircle Xenakis

[[List of probability distributions#Supported_on_semi-infinite_intervals.2C_usually_.5B0.2C.E2.88.9E.29|Continuous univariate supported on a semi-infinite interval, usually [0,∞)]]

Benini
Benktander 1st kind
Benktander 2nd kind
Beta prime
Burr
chi-squared
chi
Coxian
Dagum
Davis
EL
Erlang
exponential
F
folded normal
Flory-Schulz
Fréchet
Gamma
Gamma/Gompertz
generalized inverse Gaussian
Gompertz
half-logistic
half-normal
Hotelling's T-squared
hyper-Erlang
hyperexponential
hypoexponential
inverse chi-squared (scaled inverse chi-squared)
inverse Gaussian
inverse gamma
Kolmogorov
Lévy
log-Cauchy
log-Laplace
log-logistic
log-normal
Maxwell–Boltzmann
Maxwell–Jüttner
Mittag–Leffler
Nakagami
noncentral chi-squared
Pareto
phase-type
Poly-Weibull
Rayleigh
relativistic Breit–Wigner
Rice
Rosin–Rammler
shifted Gompertz
truncated normal
type-2 Gumbel
Weibull
Wilks' lambda

Continuous univariate supported on the whole real line (−∞, ∞)

Cauchy exponential power Fisher's z generalized normal generalized hyperbolic geometric stable Gumbel Holtsmark hyperbolic secant Johnson SU Landau Laplace Linnik logistic noncentral t normal (Gaussian) normal-inverse Gaussian skew normal slash stable Student's t type-1 Gumbel variance-gamma Voigt

Continuous univariate with support whose type varies

generalized extreme value generalized Pareto Tukey lambda q-Gaussian q-exponential shifted log-logistic

Mixed continuous-discrete univariate distributions

rectified Gaussian

Multivariate (joint)

Discrete Ewens multinomial Dirichlet-multinomial negative multinomial Continuous Dirichlet Generalized Dirichlet multivariate normal Multivariate stable multivariate Student normal-scaled inverse gamma normal-gamma Matrix-valued inverse matrix gamma inverse-Wishart matrix normal matrix t matrix gamma normal-inverse-Wishart normal-Wishart Wishart

Directional

Univariate (circular) directional Circular uniform univariate von Mises wrapped normal wrapped Cauchy wrapped exponential wrapped Lévy Bivariate (spherical) Kent Bivariate (toroidal) bivariate von Mises Multivariate von Mises–Fisher Bingham

Degenerate and singular

Degenerate discrete degenerate Dirac delta function Singular Cantor

Families

Circular compound Poisson elliptical exponential natural exponential location-scale maximum entropy mixture Pearson Tweedie wrapped

v t e Some common univariate probability distributions

Continuous	beta Cauchy chi-squared exponential F gamma Laplace log-normal normal Pareto Student's t uniform Weibull

Discrete	Bernoulli binomial discrete uniform geometric hypergeometric negative binomial Poisson

List of probability distributions

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.