Hopkins–Levitzki theorem

From Wikipedia, the free encyclopedia

In the branch of abstract algebra called ring theory, the Akizuki–Hopkins–Levitzki theorem connects the descending chain condition and ascending chain condition in modules over semiprimary rings. A ring R (with 1) is called semiprimary if R/J(R) is semisimple and J(R) is a nilpotent ideal, where J(R) denotes the Jacobson radical. The theorem states that if R is a semiprimary ring and M is an R module, the three module conditions Noetherian, Artinian and "has a composition series" are equivalent. Without the semiprimary condition, the only true implication is that if M has a composition series, then M is both Noetherian and Artinian.

The theorem takes its current form from a paper by Charles Hopkins and a paper by Jacob Levitzki, both in 1939. For this reason it is often cited as the Hopkins–Levitzki theorem. However Yasuo Akizuki is sometimes included since he proved the result for commutative rings a few years earlier (Lam 2001).

Since it is known that right Artinian rings are semiprimary, a direct corollary of the theorem is: a right Artinian ring is also right Noetherian. The analogous statement for left Artinian rings holds as well. This is not true in general for Artinian modules, because there are examples of Artinian modules which are not Noetherian.

Another direct corollary is that if R is right Artinian, then R is left Artinian if and only if it is left Noetherian.

Sketch of proof

Here is the proof of the following: Let R be a semiprimary ring and M left R-module. If M is either Artinian or Noetherian, then M has composition series.[1] (The converse of this is always true.)

Let J be the radical of R. Set 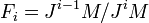F_{i}=J^{{i-1}}M/J^{i}M. The R module F_{i} may then be viewed as an R/J-module because J is contained in the annihilator of F_{i}. Each F_{i} is a semisimple R/J-module, because R/J is a semisimple ring. Furthermore since J is nilpotent, only finitely many of the F_{i} are nonzero. If M is Artinian (or Noetherian), then F_{i} has a finite composition series. Stacking the composition series from the F_{i} end to end, we obtain a composition series for M.

In Grothendieck categories

There are a number of generalizations and extensions of the theorem. One concerns Grothendieck categories: If G is a Grothendieck category with an artinian generator, then every artinian object in G is noetherian.[2]

See also

References

  1. ↑ Cohn 2003, Theorem 5.3.9
  2. ↑ Toma Albu (2010). "A Seventy Years Jubilee: The Hopkins-Levitzki Theorem". In Toma Albu. Ring and Module Theory. Springer. 
  • Cohn, P.M. (2003), Basic Algebra: Groups, Rings and Fields 
  • Charles Hopkins (1939) Rings with minimal condition for left ideals, Ann. of Math. (2) 40, pages 712–730.
  • T. Y. Lam (2001) A first course in noncommutative rings, Springer-Verlag. page 55 ISBN 0-387-95183-0
  • Jakob Levitzki (1939) On rings which satisfy the minimum condition for the right-hand ideals, Compositio Math. 7, pages 214–222.
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.