Homotopy extension property

From Wikipedia, the free encyclopedia

In mathematics, in the area of algebraic topology, the homotopy extension property indicates which homotopies defined on a subspace can be extended to a homotopy defined on a larger space.

Definition

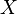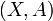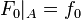Let $X\,\!$ be a topological space, and let $A\subset X$ . We say that the pair $(X,A)\,\!$ has the homotopy extension property if, given a homotopy $f_{t}\colon A\rightarrow Y$ and a map $F_{0}\colon X\rightarrow Y$ such that $F_{0}|_{A}=f_{0}$ , there exists an extension of 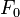$F_{0}$ to a homotopy 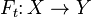$F_{t}\colon X\rightarrow Y$ such that 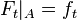$F_{t}|_{A}=f_{t}$ . ^[1]

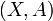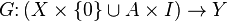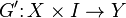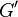That is, the pair $(X,A)\,\!$ has the homotopy extension property if any map $G\colon (X\times \{0\}\cup A\times I)\rightarrow Y$ can be extended to a map $G'\colon X\times I\rightarrow Y$ (i.e. $G\,\!$ and $G'\,\!$ agree on their common domain).

If the pair has this property only for a certain codomain 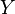$Y\,\!$ , we say that 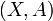$(X,A)\,\!$ has the homotopy extension property with respect to $Y\,\!$ .

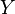Visualisation

The homotopy extension property is depicted in the following diagram

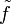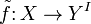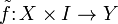If the above diagram (without the dashed map) commutes, which is equivalent to the conditions above, then there exists a map ${\tilde {f}}$ which makes the diagram commute. By currying, note that a map ${\tilde {f}}\colon X\to Y^{I}$ is the same as a map ${\tilde {f}}\colon X\times I\to Y$ .

Also compare this to the visualization of the homotopy lifting property.

Properties

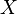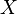If $X\,\!$ is a cell complex and $A\,\!$ is a subcomplex of $X\,\!$ , then the pair 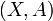$(X,A)\,\!$ has the homotopy extension property.

A pair 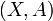$(X,A)\,\!$ has the homotopy extension property if and only if 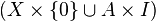$(X\times \{0\}\cup A\times I)$ is a retract of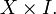 $X\times I.$

Other

If ${\mathbf {{\mathit {(X,A)}}}}$ has the homotopy extension property, then the simple inclusion map 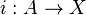$i:A\to X$ is a cofibration.

In fact, if you consider any cofibration 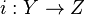$i:Y\to Z$ , then we have that ${\mathbf {{\mathit {Y}}}}$ is homeomorphic to its image under ${\mathbf {{\mathit {i}}}}$ . This implies that any cofibration can be treated as an inclusion map, and therefore it can be treated as having the homotopy extension property.

References

↑ A. Dold, Lectures on Algebraic Topology, pp. 84, Springer ISBN 3-540-58660-1

Hatcher, Allen (2002). Algebraic Topology. Cambridge University Press. ISBN 0-521-79540-0.

Homotopy extension property, PlanetMath.org.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.