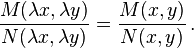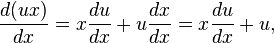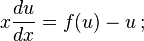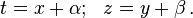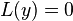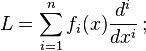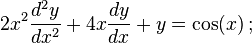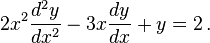Homogeneous differential equation
The term "'homogeneous'" is used in more than one context in mathematics. Perhaps the most prominent are the following three distinct cases:
- Homogeneous functions
- Homogeneous type of first order differential equations
- Homogeneous differential equations (in contrast to "inhomogeneous" differential equations). This definition is used to define a property of certain linear differential equations—it is unrelated to the above two cases.
Each one of these cases will be briefly explained as follows.
Homogeneous functions
Definition. A function  is said to be homogeneous of degree
is said to be homogeneous of degree  if, by introducing a constant parameter
if, by introducing a constant parameter 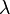 , replacing the variable
, replacing the variable  with
with 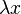 we find:
we find:
This definition can be generalized to functions of more-than-one variables; for example, a function of two variables  is said to be homogeneous of degree
is said to be homogeneous of degree  if we replace both variables
if we replace both variables  and
and  by
by 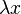 and
and 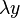 , we find:
, we find:
Example. The function  is a homogeneous function of degree 2 because:
is a homogeneous function of degree 2 because:
This definition of homogeneous functions has been used to classify certain types of first order differential equations.
Homogeneous type of first-order differential equations
| Differential equations |
|---|
| Classification |
|
Operations
|
|
Attributes of variables
|
|
Relation to processes
|
| Solutions |
|
Solution topics
|
A first-order ordinary differential equation in the form:
is a homogeneous type if both functions M(x, y) and N(x, y) are homogeneous functions of the same degree n.[1] That is, multiplying each variable by a parameter 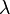 , we find:
, we find:
 and
and 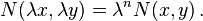
Thus,
Solution method
In the quotient 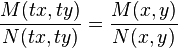 ,
we can let
,
we can let 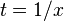 to simplify this quotient to a function
to simplify this quotient to a function  of the single variable
of the single variable 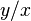 :
:
Introduce the change of variables 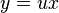 ; differentiate using the product rule:
; differentiate using the product rule:
thus transforming the original differential equation into the separable form:
this form can now be integrated directly (see ordinary differential equation).
Special case
A first order differential equation of the form (a, b, c, e, f, g are all constants):
can be transformed into a homogeneous type by a linear transformation of both variables ( and
and  are constants):
are constants):
Homogeneous linear differential equations
Definition. A linear differential equation is called homogeneous if the following condition is satisfied: If 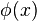 is a solution, so is
is a solution, so is 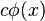 , where
, where  is an arbitrary (non-zero) constant. Note that in order for this condition to hold, each term in a linear differential equation of the dependent variable y must contain y or any derivative of y; a constant term breaks homogeneity. A linear differential equation that fails this condition is called inhomogeneous.
is an arbitrary (non-zero) constant. Note that in order for this condition to hold, each term in a linear differential equation of the dependent variable y must contain y or any derivative of y; a constant term breaks homogeneity. A linear differential equation that fails this condition is called inhomogeneous.
A linear differential equation can be represented as a linear operator acting on y(x) where x is usually the independent variable and y is the dependent variable. Therefore, the general form of a linear homogeneous differential equation is of the form:
where L is a differential operator, a sum of derivatives, each multiplied by a function  of x:
of x:
where  may be constants, but not all
may be constants, but not all  may be zero.
may be zero.
For example, the following differential equation is homogeneous
whereas the following two are inhomogeneous:
See also
- Method of separation of variables
Notes
- ↑ Ince 1956, p. 18
References
- Boyce, William E.; DiPrima, Richard C. (2012), Elementary differential equations and boundary value problems (10th ed.), Wiley, ISBN 978-0470458310. (This is a good introductory reference on differential equations.)
- Ince, E. L. (1956), Ordinary differential equations, New York: Dover Publications, ISBN 0486603490. (This is a classic reference on ODEs, first published in 1926.)
External links
- Homogeneous differential equations at MathWorld
- Wikibooks: Ordinary Differential Equations/Substitution 1
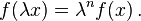

![f(\lambda x,\lambda y)=[2(\lambda x)^{2}-3(\lambda y)^{2}+4(\lambda x\lambda y)]=(2\lambda ^{2}x^{2}-3\lambda ^{2}y^{2}+4\lambda ^{2}xy)=\lambda ^{2}(2x^{2}-3y^{2}+4xy)=\lambda ^{2}f(x,y).](/2014-wikipedia_en_all_02_2014/I/media/1/d/d/4/1dd4303aae127bdfaf6aa86bb0101449.png)