High-dimensional statistics

In statistical theory, the field of high-dimensional statistics studies data whose dimension is larger than dimensions considered in classical multivariate analysis. High-dimensional statistics relies on the theory of random vectors. In many applications, the dimension of the data vectors may be larger than the sample size.

History

Traditionally, statistical inference considers a probability model for a population and considers data that arose as a sample from the population. For many problems, the estimates of the population characteristics ("parameters") can be substantially refined (in theory) as the sample size increases toward infinity. A traditional requirement of estimators is consistency, that is, the convergence to the unknown true value of the parameter.

In 1968, A.N.Kolmogorov proposed another setting of statistical problems and another setting for the asymptotics, in which the dimension of variables p increases along with the sample size n so that the ratio p/n tends to a constant. It was called the “increasing dimension asymptotics” or “the Kolmogorov asymptotics”^[1] Kolmogorov's approach makes it possible to isolate many principal terms of error probabilities and of standard measures of the quality of estimators (quality functions) for large p and n.

Recently, researchers are more interested in even larger dimension cases, e.g. 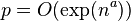, where . This field emerges from the need of extracting meaningful information from many different areas.

Mathematical theory

Extensive mathematical investigations were carried out that resulted in the creation of systematic theory for improved and asymptotically unimprovable versions of multivariate statistical procedures (see references at ^[2]). A special parameter G that is a function of the fourth moments of variables was found having the property that a small value of G produces a number of specifically many-parametric phenomena. For increasing p and n so that p/n tends to a constant and G → 0, the principal terms of rotation invariant functionals occurring in statistics prove to be dependent on only the first two moments of variables. Under n and p tending to infinity, p/n → y > 0, and G → 0, these functionals have vanishing variance and converge to constants that represent the limit value of empirical means and variances. As a consequence, some stable integral relations are produced between functions of parameters and functions of observable variables. They were called “stochastic canonical equations” or “dispersion equations”.^[3] Using them one can express the principle parts of standard quality functions of regularized multivariate statistical procedures as functions of only observed variables. This provides the possibility of choosing better procedures and finding asymptotically unimprovable solutions.

Current developments

High-dimensional statistics has been the focus of many seminars and workshops.^[4][5][6][7]

Notes

References

• T. Tony Cai, Xiaotong Shen, ed. (2011). High-dimensional data analysis. Frontiers of Statistics. Singapore: World Scientific. 

• Peter Bühlmann and Sara van de Geer (2011). Statistics for high-dimensional data: methods, theory and applications. Heidelberg; New York: Springer.