Hereditarily countable set
In set theory, a set is called hereditarily countable if it is a countable set of hereditarily countable sets. This inductive definition is in fact well-founded and can be expressed in the language of first-order set theory. A set is hereditarily countable if and only if it is countable, and every element of its transitive closure is countable. If the axiom of countable choice holds, then a set is hereditarily countable if and only if its transitive closure is countable.
The class of all hereditarily countable sets can be proven to be a set from the axioms of Zermelo–Fraenkel set theory (ZF) without any form of the axiom of choice, and this set is designated 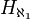 . The hereditarily countable sets form a model of Kripke–Platek set theory with the axiom of infinity (KPI), if the axiom of countable choice is assumed in the metatheory.
. The hereditarily countable sets form a model of Kripke–Platek set theory with the axiom of infinity (KPI), if the axiom of countable choice is assumed in the metatheory.
If  , then
, then 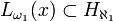 .
.
More generally, a set is hereditarily of cardinality less than κ if and only it is of cardinality less than κ, and all its elements are hereditarily of cardinality less than κ; the class of all such sets can also be proven to be a set from the axioms of ZF, and is designated 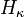 . If the axiom of choice holds and the cardinal κ is regular, then a set is hereditarily of cardinality less than κ if and only if its transitive closure is of cardinality less than κ.
. If the axiom of choice holds and the cardinal κ is regular, then a set is hereditarily of cardinality less than κ if and only if its transitive closure is of cardinality less than κ.