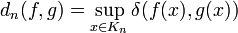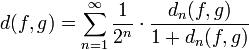Hemicompact space

From Wikipedia, the free encyclopedia

In mathematics, in the field of topology, a topological space is said to be hemicompact if it has a sequence of compact subsets such that every compact subset of the space lies inside some compact set in the sequence. Clearly, this forces the union of the sequence to be the whole space, because every point is compact and hence must lie in one of the compact sets.

Examples

Properties

Every first countable hemicompact space is locally compact.

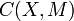If X is a hemicompact space, then the space C(X,M) of all continuous functions 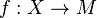f:X\to M to a metric space 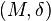(M,\delta ) with the compact-open topology is metrizable. To see this, take a sequence 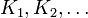K_{1},K_{2},\dots of compact subsets of X such that every compact subset of X lies inside some compact set in this sequence (the existence of such a sequence follows from the hemicompactness of X). Denote

d_{n}(f,g)=\sup _{{x\in K_{n}}}\delta (f(x),g(x))

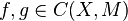for f,g\in C(X,M) and n\in {\mathbb {N}}. Then

d(f,g)=\sum _{{n=1}}^{{\infty }}{\frac {1}{2^{n}}}\cdot {\frac {d_{n}(f,g)}{1+d_{n}(f,g)}}

defines a metric on 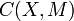C(X,M) which induces the compact-open topology.

See also

References

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.