Helicity (particle physics)

From Wikipedia, the free encyclopedia

In particle physics, helicity is the projection of the spin 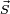\scriptstyle {\vec S} onto the direction of momentum, \scriptstyle {\hat p}:

h={\vec J}\cdot {\hat p}={\vec L}\cdot {\hat p}+{\vec S}\cdot {\hat p}={\vec S}\cdot {\hat p},\qquad {\hat p}={\frac {{\vec p}}{\left|{\vec p}\right|}}

as the projection of orbital angular momentum along the linear momentum is zero, 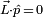\scriptstyle {\vec L}\cdot {\hat p}\,=\,0. Because the eigenvalues of spin with respect to an axis have discrete values, the eigenvalues of helicity are also discrete. For a particle of spin S, the eigenvalues of helicity are S, S − 1, ..., −S. The measured helicity of a spin S particle will range from −S to +S.

In 3 + 1 dimensions, the little group for a massless particle is the double cover of SE(2). This has unitary representations which are invariant under the SE(2) "translations" and transform as eihθ under a SE(2) rotation by θ. This is the helicity h representation. There is also another unitary representation which transforms non-trivially under the SE(2) translations. This is the continuous spin representation.

In d + 1 dimensions, the little group is the double cover of SE(d − 1) (the case where d ≤ 2 is more complicated because of anyons, etc.). As before, there are unitary representations which don't transform under the SE(d − 1) "translations" (the "standard" representations) and "continuous spin" representations.

For massless spin-1⁄2 particles, helicity is equivalent to the chirality operator multiplied by 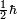\scriptstyle {\frac {1}{2}}\hbar .

See also

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.