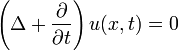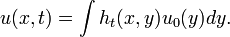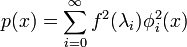Heat kernel signature

From Wikipedia, the free encyclopedia

A heat kernel signature (HKS) is a feature descriptor for use in deformable shape analysis and belongs to the group of spectral shape analysis methods. For each point in the shape, HKS defines its feature vector representing the point's local and global geometric properties. Applications include segmentation, classification, structure discovery, shape matching and shape retrieval.

HKS was introduced in 2009 by Jian Sun, Maks Ovsjanikov and Leonidas Guibas.^[1] It is based on heat kernel, which is a fundamental solution to the heat equation. HKS is one of the many recently introduced shape descriptors which are based on the Laplace–Beltrami operator associated with the shape.^[2]

Overview

Shape analysis is the field of automatic digital analysis of shapes, e.g., 3D objects. For many shape analysis tasks (such as shape matching/retrieval), feature vectors for certain key points are used instead of using the complete 3D model of the shape. An important requirement of such feature descriptors is for them to be invariant under certain transformations. For rigid transformations, commonly used feature descriptors include shape context, spin images, integral volume descriptors and multiscale local features, among others.^[2] HKS allows isometric transformations which generalizes rigid transformations.

HKS is based on the concept of heat diffusion over a surface. Given an initial heat distribution 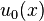$u_{0}(x)$ over the surface, the heat kernel 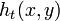$h_{t}(x,y)$ relates the amount of heat transferred from $x$ to $y$ after time $t$ . 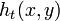The heat kernel is invariant under isometric transformations and stable under small perturbations to the isometry.^[1] In addition, the heat kernel fully characterizes shapes up to an isometry and represents increasingly global properties of the shape with increasing time.^[3] Since $h_{t}(x,y)$ is defined for a pair of points over a temporal domain, using heat kernels directly as features would lead to a high complexity. HKS instead restricts itself to just the temporal domain by considering only 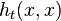$h_{t}(x,x)$ . HKS inherits most of the properties of heat kernels under certain conditions.^[1]

Technical details

The heat diffusion equation over a compact Riemannian manifold $M$ (possibly with a boundary) is given by,

$\left(\Delta +{\frac {\partial }{\partial t}}\right)u(x,t)=0$

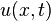where $\Delta$ is the Laplace–Beltrami operator and $u(x,t)$ is the heat distribution at a point $x$ at time $t$ . The solution to this equation can be expressed as,^[1]

$u(x,t)=\int h_{t}(x,y)u_{0}(y)dy.$

The eigen decomposition of the heat kernel is expressed as,

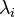$h_{t}(x,y)=\sum _{{i=0}}^{{\infty }}\exp(-\lambda _{i}t)\phi _{i}(x)\phi _{i}(y)$

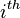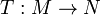where $\lambda _{i}$ and $\phi _{i}$ are the $i^{{th}}$ eigenvalue and eigenfunction of $\Delta$ . The heat kernel fully characterizes a surface up to an isometry: For any surjective map $T:M\rightarrow N$ between two Riemannian manifolds $M$ and $N$ , if $h_{t}(x,y)=h_{t}(T(x),T(y))$ then $T$ is an isometry, and vice-versa.^[1] For a concise feature descriptor, HKS restricts the heat kernel only to the temporal domain,

$h_{t}(x,x)=\sum _{{i=0}}^{{\infty }}\exp(-\lambda _{i}t)\phi _{i}^{2}(x).$

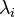HKS, similar to the heat kernel, characterizes surfaces under the condition that the eigenvalues of $\Delta$ for $M$ and $N$ are non-repeating. The terms $\exp(-\lambda _{i}t)$ can be intuited as a bank of low-pass filters, with $\lambda _{i}$ determining the cutoff frequencies.^[2]

Practical considerations

Since 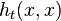$h_{t}(x,x)$ is, in general, a non-parametric continuous function, HKS is in practice represented as a discrete sequence of $\{h_{{t_{1}}}(x,x),\ldots ,h_{{t_{n}}}(x,x)\}$ values sampled at times $t_{1},\ldots ,t_{n}$ .

In most applications, the underlying manifold for an object is not known. The HKS can be computed if a mesh representation of the manifold is available, by using a discrete approximation to $\Delta$ and using the discrete analogue of the heat equation. In the discrete case, the Laplace–Beltrami operator is a sparse matrix and can be written as,^[1]

$L=A^{{-1}}W$

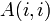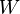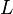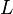where $A$ is a positive diagonal matrix with entries $A(i,i)$ corresponding to the area of the triangles in the mesh sharing the vertex $i$ , and $W$ is a symmetric semi-definite weighting matrix. $L$ can be decomposed into $L=\Phi \Lambda \Phi ^{T}A$ , where $\Lambda$ is a diagonal matrix of the eigenvalues of $L$ arranged in the ascending order, and $\Phi$ is the matrix with the corresponding orthonormal eigenvectors. The discrete heat kernel is the matrix given by,

$K_{t}=\Phi \exp(-t\Lambda )\Phi ^{T}.$

The elements $k_{t}(i,j)$ represents the heat diffusion between vertices $i$ and $j$ after time $t$ . The HKS is then given by the diagonal entries of this matrix, sampled at discrete time intervals. Similar to the continuous case, the discrete HKS is robust to noise.^[1]

Limitations

Non-repeating eigenvalues

The main property that characterizes surfaces using HKS up to an isometry holds only when the eigenvalues of the surfaces are non-repeating. There are certain surfaces (especially those with symmetry) where this condition is violated. A sphere is a simple example of such a surface.

Time parameter selection

The time parameter in the HKS is closely related to the scale of global information. However, there is no direct way to choose the time discretization. The existing method chooses time samples logarithmically which is a heuristic with no guarantees^[4]

Time complexity

The discrete heat kernel requires eigendecomposition of a matrix of size 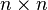$n\times n$ , where $n$ is the number of vertices in the mesh representation of the manifold. Computing the eigendecomposition is an expensive operation, especially as $n$ increases. Note, however, that because of the inverse exponential dependence on the eigenvalue, typically only a small (less than 100) eigenvectors are sufficient to obtain a good approximation of the HKS.

Non-isometric transformations

The performance guarantees for HKS only hold for truly isometric transformations. However, deformations for real shapes are often not isometric. A simple example of such transformation is closing of the fist by a person, where the geodesic distances between two fingers changes.

Relation with other methods^[2]

Curvature

The (continuous) HKS at a point 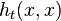$x$ , $h_{t}(x,x)$ on the Riemannian manifold is related to the scalar curvature $s(x)$ by,

$h_{t}(x,x)={\frac {1}{4\pi t}}+{\frac {s(x)}{12\pi }}+O(t).$

Hence, HKS can as be interpreted as the curvature of $x$ at scale $t$ .

Wave kernel signature (WKS)

The WKS^[4] follows a similar idea to the HKS, replacing the heat equation with the Schrödinger wave equation,

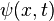$\left(i\Delta +{\frac {\partial }{\partial t}}\right)\psi (x,t)=0$

where $\psi (x,t)$ is the complex wave function. The average probability of measuring the particle at a point $x$ is given by,

$p(x)=\sum _{{i=0}}^{{\infty }}f^{2}(\lambda _{i})\phi _{i}^{2}(x)$

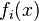where $f$ is the initial energy distribution. By fixing a family of this energy distributions $f_{i}(x)$ , the WKS can be obtained as a discrete sequence 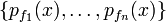$\{p_{{f_{1}}}(x),\ldots ,p_{{f_{n}}}(x)\}$ . Unlike HKS, the WKS can be intuited as a set of band-pass filters leading to better feature localization. However, the WKS does not represent large-scale features well (as they are filtered out) yielding poor performance at shape matching applications.

Global point signature (GPS)

Similar to the HKS, the GPS^[5] is based on the Laplace-Beltrami operator. GPS at a point $x$ is a vector of scaled eigenfunctions of the Laplace–Beltrami operator computed at $x$ . The GPS is a global feature whereas the scale of the HKS can be varied by varying the time parameter for heat diffusion. Hence, the HKS can be used in partial shape matching applications whereas the GPS cannot.

Extensions

Scale invariance

Even though the HKS represents the shape at multiple scales, it is not inherently scale invariant. For example, the HKS for a shape and its scaled version are not the same without pre-normalization. A simple way to ensure scale invariance is by pre-scaling each shape to have the same surface area (e.g. 1). Using the notation above, this means:

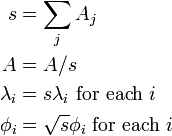
${\begin{aligned}s&=\sum _{j}A_{j}\\A&=A/s\\\lambda _{i}&=s\lambda _{i}{\text{ for each }}i\\\phi _{i}&={\sqrt {s}}\phi _{i}{\text{ for each }}i\\\end{aligned}}$

Alternatively, scale-invariant version of the HKS can also be constructed by generating a Scale space representation.^[6] In the scale-space, the HKS of a scaled shape corresponds to a translation up to a multiplicative factor. The fourier transform of this HKS changes the time-translation into the complex plane, and the dependency on translation can be eliminated by considering the modulus of the transform. Demo of Scale-invariant HKS on YouTube

Volumetric HKS

The HKS is defined for a boundary surface of a 3D shape, represented as a 2D Riemannian manifold. Instead of considering only the boundary, the entire volume of the 3D shape can be considered to define the volumetric version of the HKS.^[7] The Volumetric HKS is defined analogous to the normal HKS by considering the heat equation over the entire volume (as a 3-submanifold) and defining a Neumann boundary condition over the 2-manifold boundary of the shape. Volumetric HKS characterizes transformations up to a volume isometry, which represent the transformation for real 3D objects more faithfully than boundary isometry.^[7]

Shape Search

The scale-invariant HKS features can be used in the bag-of-features model for shape retrieval applications.^[8] The features are used to construct geometric words by taking into account their spatial relations, from which shapes can be constructed (analogous to using features as words and shapes as sentences). Shapes themselves are represented using compact binary codes to form an indexed collection. Given a query shape, similar shapes in the index with possibly isometric transformations can be retrieved by using the Hamming distance of the code as the nearness-measure.

References

↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 Sun, J. and Ovsjanikov, M. and Guibas, L. (2009). "A Concise and Provably Informative Multi-Scale Signature-Based on Heat Diffusion". Computer Graphics Forum 28 (5). pp. 1383–1392.
↑ 2.0 2.1 2.2 2.3 Alexander M. Bronstein (2011). "Spectral descriptors for deformable shapes". CoRR. abs/1110.5015.
↑ Grigor'yan, A. (2006). "Heat kernels on weighted manifolds and applications". Contemporary Mathematics 398: 93–191.
↑ 4.0 4.1 Aubry, M. and Schlickewei, U. and Cremers, D. (2011). "The Wave Kernel Signature—A Quantum Mechanical Approach to Shape Analyis". IEEE International Conference on Computer Vision (ICCV) - Workshop on Dynamic Shape Capture and Analysis (4DMOD).
↑ Rustamov, R.M. (2007). "Laplace–Beltrami eigenfunctions for deformation invariant shape representation". Proceedings of the fifth Eurographics symposium on Geometry processing. pp. 225–233. Unknown parameter |organization= ignored (help)
↑ Bronstein, M.M. and Kokkinos, I. (2010). "Scale-invariant heat kernel signatures for non-rigid shape recognition". Computer Vision and Pattern Recognition (CVPR), 2010. pp. 1704–1711. Unknown parameter |organization= ignored (help)
↑ 7.0 7.1 Raviv, D. and Bronstein, M.M. and Bronstein, A.M. and Kimmel, R. (2010). "Volumetric heat kernel signatures". Proceedings of the ACM workshop on 3D object retrieval. pp. 30–44. Unknown parameter |organization= ignored (help)
↑ Bronstein, A.M. and Bronstein, M.M. and Guibas, L.J. and Ovsjanikov, M. (2011). "Shape google: Geometric words and expressions for invariant shape retrieval". ACM Transactions on Graphics (TOG) (ACM) 30 (1).

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.