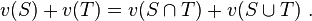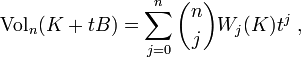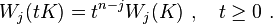Hadwiger's theorem
In integral geometry (otherwise called geometric probability theory), Hadwiger's theorem characterises the valuations on convex bodies in Rn. It was proved by Hugo Hadwiger.
Introduction
Valuations
Let Kn be the collection of all compact convex sets in Rn. A valuation is a function v:Kn → R such that v(∅) = 0 and, for every S,T ∈Kn for which S∪T∈Kn,
A valuation is called continuous if it is continuous with respect to the Hausdorff metric. A valuation is called invariant under rigid motions if v(φ(S)) = v(S) whenever S ∈ Kn and φ is either a translation or a rotation of Rn.
Quermassintegrals
The quermassintegrals Wj: Kn → R are defined via Steiner's formula
where B is the Euclidean ball. For example, W0 is the volume, W1 is proportional to the surface measure, Wn-1 is proportional to the mean width, and Wn is the constant Voln(B).
Wj is a valuation which is homogeneous of degree n-j, that is,
Statement
Any continuous valuation v on Kn that is invariant under rigid motions can be represented as
Corollary
Any continuous valuation v on Kn that is invariant under rigid motions and homogeneous of degree j is a multiple of Wn-j.
References
An account and a proof of Hadwiger's theorem may be found in
- Klain, D.A.; Rota, G.-C. (1997). Introduction to geometric probability. Cambridge: Cambridge University Press. ISBN 0-521-59362-X. MR 1608265.
An elementary and self-contained proof was given by Beifang Chen in
- Chen, B. (2004). "A simplified elementary proof of Hadwiger's volume theorem". Geom. Dedicata 105: 107–120. MR 2057247.