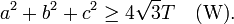Hadwiger–Finsler inequality

From Wikipedia, the free encyclopedia

In mathematics, the Hadwiger–Finsler inequality is a result on the geometry of triangles in the Euclidean plane, named after the mathematicians Hugo Hadwiger and Paul Finsler. It states that if a triangle in the plane has side lengths a, b and c and area T, then

$a^{{2}}+b^{{2}}+c^{{2}}\geq (a-b)^{{2}}+(b-c)^{{2}}+(c-a)^{{2}}+4{\sqrt {3}}T\quad {\mbox{(HF)}}.$

Weitzenböck's inequality is a straightforward corollary of the Hadwiger–Finsler inequality: if a triangle in the plane has side lengths a, b and c and area T, then

$a^{{2}}+b^{{2}}+c^{{2}}\geq 4{\sqrt {3}}T\quad {\mbox{(W)}}.$

Weitzenböck's inequality can also be proved using Heron's formula, by which route it can be seen that equality holds in (W) if and only if the triangle is an equilateral triangle, i.e. a = b = c.

The Hadwiger–Finsler inequality is a special case of Pedoe's inequality.

References

Finsler, Paul; Hadwiger, Hugo (1937). "Einige Relationen im Dreieck". Commentarii Mathematici Helvetici 10 (1): 316–326. doi:10.1007/BF01214300. Cite uses deprecated parameters (help)

External links

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.