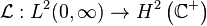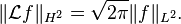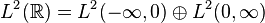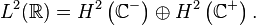H square
In mathematics and control theory, H2, or H-square is a Hardy space with square norm. It is a subspace of L2 space, and is thus a Hilbert space. In particular, it is a reproducing kernel Hilbert space.
On the unit circle
In general, elements of L2 on the unit circle are given by
whereas elements of H2 are given by
The projection from L2 to H2 (by setting an = 0 when n < 0) is orthogonal.
On the half-plane
The Laplace transform  given by
given by
can be understood as a linear operator
where 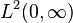 is the set of square-integrable functions on the positive real number line, and
is the set of square-integrable functions on the positive real number line, and 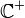 is the right half of the complex plane. It is more; it is an isomorphism, in that it is invertible, and it isometric, in that it satisfies
is the right half of the complex plane. It is more; it is an isomorphism, in that it is invertible, and it isometric, in that it satisfies
The Laplace transform is "half" of a Fourier transform; from the decomposition
one then obtains an orthogonal decomposition of  into two Hardy spaces
into two Hardy spaces
This is essentially the Paley-Wiener theorem.
See also
- H∞
References
- Jonathan R. Partington, "Linear Operators and Linear Systems, An Analytical Approach to Control Theory", London Mathematical Society Student Texts 60, (2004) Cambridge University Press, ISBN 0-521-54619-2.
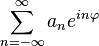

=\int _{0}^{\infty }e^{{-st}}f(t)dt](/2014-wikipedia_en_all_02_2014/I/media/3/e/4/b/3e4b94db824c36a7c3ad36f1e0c48038.png)