Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of reflections. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example. However, not all Coxeter groups are finite, and not all can be described in terms of symmetries and Euclidean reflections. Coxeter groups were introduced (Coxeter 1934) as abstractions of reflection groups, and finite Coxeter groups were classified in 1935 (Coxeter 1935).
Coxeter groups find applications in many areas of mathematics. Examples of finite Coxeter groups include the symmetry groups of regular polytopes, and the Weyl groups of simple Lie algebras. Examples of infinite Coxeter groups include the triangle groups corresponding to regular tessellations of the Euclidean plane and the hyperbolic plane, and the Weyl groups of infinite-dimensional Kac–Moody algebras.
Standard references include (Humphreys 1990) and (Davis 2007).
Definition
Formally, a Coxeter group can be defined as a group with the presentation
where  and
and  for
for  .
The condition
.
The condition  means no relation of the form
means no relation of the form  should be imposed.
should be imposed.
The pair (W,S) where W is a Coxeter group with generators S={r1,...,rn} is called Coxeter system. Note that in general S is not uniquely determined by W. For example, the Coxeter groups of type BC3 and A1xA3 are isomorphic but the Coxeter systems are not equivalent (see below for an explanation of this notation).
A number of conclusions can be drawn immediately from the above definition.
- The relation mi i = 1 means that (riri )1 = (ri )2 = 1 for all i ; the generators are involutions.
- If mi j = 2, then the generators ri and rj commute. This follows by observing that
- xx = yy = 1,
- together with
- xyxy = 1
- implies that
- xy = x(xyxy)y = (xx)yx(yy) = yx.
- Alternatively, since the generators are involutions,
 , so
, so  , and thus is equal to the commutator.
, and thus is equal to the commutator.
- In order to avoid redundancy among the relations, it is necessary to assume that mi j = mj i. This follows by observing that
- yy = 1,
- together with
- (xy)m = 1
- implies that
- (yx)m = (yx)myy = y(xy)my = yy = 1.
- Alternatively,
 and
and  are conjugate elements, as
are conjugate elements, as  .
.
Coxeter matrix and Schläfli matrix
The Coxeter matrix is the n×n, symmetric matrix with entries mi j. Indeed, every symmetric matrix with positive integer and ∞ entries and with 1's on the diagonal such that all nondiagonal entries are greater than 1 serves to define a Coxeter group.
The Coxeter matrix can be conveniently encoded by a Coxeter diagram, as per the following rules.
- The vertices of the graph are labelled by generator subscripts.
- Vertices i and j are connected if and only if mi j ≥ 3.
- An edge is labelled with the value of mi j whenever it is 4 or greater.
In particular, two generators commute if and only if they are not connected by an edge. Furthermore, if a Coxeter graph has two or more connected components, the associated group is the direct product of the groups associated to the individual components. Thus the disjoint union of Coxeter graphs yields a direct product of Coxeter groups.
The Coxeter matrix, Mi,j, is related to the Schläfli matrix, Ci,j, but the elements are modified, being proportional to the dot product of the pairwise generators: Schläfli matrix Ci,j=-2cos(π/Mi,j). The Schläfli matrix is useful because its eigenvalues determine whether the Coxeter group is of finite type (all positive), affine type (all non-negative, at least one zero), or indefinite type (otherwise). The indefinite type is sometimes further subdivided, e.g. into hyperbolic and other Coxeter groups. However, there are multiple non-equivalent definitions for hyperbolic Coxeter groups.
| Coxeter group | A1×A1 | A2 |  |
A3 | BC3 | D4 |  |
|---|---|---|---|---|---|---|---|
| Coxeter diagram | |||||||
| Coxeter matrix | ![\left[{\begin{smallmatrix}1&2\\2&1\\\end{smallmatrix}}\right]](/2014-wikipedia_en_all_02_2014/I/media/c/d/f/9/cdf96a316bc9df8570dd9635095ce975.png) |
![\left[{\begin{smallmatrix}1&3\\3&1\\\end{smallmatrix}}\right]](/2014-wikipedia_en_all_02_2014/I/media/c/f/4/a/cf4a82ec09747ea06fc8101c60f04fd8.png) |
![\left[{\begin{smallmatrix}1&\infty \\\infty &1\\\end{smallmatrix}}\right]](/2014-wikipedia_en_all_02_2014/I/media/a/9/d/2/a9d2e1faffe30f832e71193a00aaae3c.png) |
![\left[{\begin{smallmatrix}1&3&2\\3&1&3\\2&3&1\end{smallmatrix}}\right]](/2014-wikipedia_en_all_02_2014/I/media/0/8/d/a/08da0b84ff3898018a900911668d7195.png) |
![\left[{\begin{smallmatrix}1&4&2\\4&1&3\\2&3&1\end{smallmatrix}}\right]](/2014-wikipedia_en_all_02_2014/I/media/e/a/e/b/eaebf6fbc821ea0a2f988a58066b4976.png) |
![\left[{\begin{smallmatrix}1&3&2&2\\3&1&3&3\\2&3&1&2\\2&3&2&1\end{smallmatrix}}\right]](/2014-wikipedia_en_all_02_2014/I/media/6/7/1/5/67158bf41a0be04bf20b966271b78769.png) |
![\left[{\begin{smallmatrix}1&3&2&3\\3&1&3&2\\2&3&1&3\\3&2&3&1\end{smallmatrix}}\right]](/2014-wikipedia_en_all_02_2014/I/media/a/6/7/f/a67f871ae3c45940d395029afa1a814d.png) |
| Schläfli matrix | ![\left[{\begin{smallmatrix}2&0\\0&2\end{smallmatrix}}\right]](/2014-wikipedia_en_all_02_2014/I/media/d/3/4/8/d3483b4cea4bad9214a96818c8c94458.png) |
![\left[{\begin{smallmatrix}2&-1\\-1&2\end{smallmatrix}}\right]](/2014-wikipedia_en_all_02_2014/I/media/1/3/1/3/13133ff56fb693a8182b3b229c32cac6.png) |
![\left[{\begin{smallmatrix}2&-2\\-2&2\end{smallmatrix}}\right]](/2014-wikipedia_en_all_02_2014/I/media/b/0/1/c/b01c478b024bc2a95139bd38ae5ccf03.png) |
![\left[{\begin{smallmatrix}2&-1&0\\-1&2&-1\\0&-1&2\end{smallmatrix}}\right]](/2014-wikipedia_en_all_02_2014/I/media/9/7/3/a/973a70e75bd63b1adeca056f131fd3d8.png) |
![\left[{\begin{smallmatrix}2&-{\sqrt {2}}&0\\-{\sqrt {2}}&2&-1\\0&-1&2\end{smallmatrix}}\right]](/2014-wikipedia_en_all_02_2014/I/media/3/b/0/5/3b0556884cfde28bb22ea2fffb030605.png) |
![\left[{\begin{smallmatrix}2&-1&0&0\\-1&2&-1&-1\\0&-1&2&0\\0&-1&0&2\end{smallmatrix}}\right]](/2014-wikipedia_en_all_02_2014/I/media/4/a/4/a/4a4a278f10a2e08966f1e2813a45b4a3.png) |
![\left[{\begin{smallmatrix}2&-1&0&-1\\-1&2&-1&0\\0&-1&2&-1\\-1&0&-1&2\end{smallmatrix}}\right]](/2014-wikipedia_en_all_02_2014/I/media/c/9/b/b/c9bbb8390ce29115511e9378e1adc277.png) |
An example
The graph in which vertices 1 through n are placed in a row with each vertex connected by an unlabelled edge to its immediate neighbors gives rise to the symmetric group Sn+1; the generators correspond to the transpositions (1 2), (2 3), ... (n n+1). Two non-consecutive transpositions always commute, while (k k+1) (k+1 k+2) gives the 3-cycle (k k+2 k+1). Of course this only shows that Sn+1 is a quotient group of the Coxeter group described by the graph, but it is not too difficult to check that equality holds.
Connection with reflection groups
Coxeter groups are deeply connected with reflection groups. Simply put, Coxeter groups are abstract groups (given via a presentation), while reflection groups are concrete groups (given as subgroups of linear groups or various generalizations). Coxeter groups grew out of the study of reflection groups — they are an abstraction: a reflection group is a subgroup of a linear group generated by reflections (which have order 2), while a Coxeter group is an abstract group generated by involutions (elements of order 2, abstracting from reflections), and whose relations have a certain form ( , corresponding to hyperplanes meeting at an angle of
, corresponding to hyperplanes meeting at an angle of  , with
, with  being of order k abstracting from a rotation by
being of order k abstracting from a rotation by  ).
).
The abstract group of a reflection group is a Coxeter group, while conversely a reflection group can be seen as a linear representation of a Coxeter group. For finite reflection groups, this yields an exact correspondence: every finite Coxeter group admits a faithful representation as a finite reflection group of some Euclidean space. For infinite Coxeter groups, however, a Coxeter group may not admit a representation as a reflection group.
Historically, (Coxeter 1934) proved that every reflection group is a Coxeter group (i.e., has a presentation where all relations are of the form  or
or  ), and indeed this paper introduced the notion of a Coxeter group, while (Coxeter 1935) proved that every finite Coxeter group had a representation as a reflection group, and classified finite Coxeter groups.
), and indeed this paper introduced the notion of a Coxeter group, while (Coxeter 1935) proved that every finite Coxeter group had a representation as a reflection group, and classified finite Coxeter groups.
Finite Coxeter groups

Classification
The finite Coxeter groups were classified in (Coxeter 1935), in terms of Coxeter–Dynkin diagrams; they are all represented by reflection groups of finite-dimensional Euclidean spaces.
The finite Coxeter groups consist of three one-parameter families of increasing rank  one one-parameter family of dimension two,
one one-parameter family of dimension two,  and six exceptional groups:
and six exceptional groups: 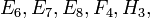 and
and 
Weyl groups
Many, but not all of these, are Weyl groups, and every Weyl group can be realized as a Coxeter group. The Weyl groups are the families  and
and  and the exceptions
and the exceptions  and
and  denoted in Weyl group notation as
denoted in Weyl group notation as  The non-Weyl groups are the exceptions
The non-Weyl groups are the exceptions 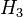 and
and  and the family
and the family  except where this coincides with one of the Weyl groups (namely
except where this coincides with one of the Weyl groups (namely  and
and  ).
).
This can be proven by comparing the restrictions on (undirected) Dynkin diagrams with the restrictions on Coxeter diagrams of finite groups: formally, the Coxeter graph can be obtained from the Dynkin diagram by discarding the direction of the edges, and replacing every double edge with an edge labelled 4 and every triple edge by an edge labelled 6. Also note that every finitely generated Coxeter group is an Automatic group.[1] Dynkin diagrams have the additional restriction that the only permitted edge labels are 2, 3, 4, and 6, which yields the above. Geometrically, this corresponds to the crystallographic restriction theorem, and the fact that excluded polytopes do not fill space or tile the plane – for  the dodecahedron (dually, icosahedron) does not fill space; for
the dodecahedron (dually, icosahedron) does not fill space; for  the 120-cell (dually, 600-cell) does not fill space; for
the 120-cell (dually, 600-cell) does not fill space; for  a p-gon does not tile the plane except for
a p-gon does not tile the plane except for  or
or 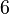 (the triangular, square, and hexagonal tilings, respectively).
(the triangular, square, and hexagonal tilings, respectively).
Note further that the (directed) Dynkin diagrams Bn and Cn give rise to the same Weyl group (hence Coxeter group), because they differ as directed graphs, but agree as undirected graphs – direction matters for root systems but not for the Weyl group; this corresponds to the hypercube and cross-polytope being different regular polytopes but having the same symmetry group.
Properties
Some properties of the finite Coxeter groups are given in the following table:
| Group symbol | Alternate symbol | Bracket notation | Rank | Order | Related polytopes | Coxeter-Dynkin diagram |
|---|---|---|---|---|---|---|
| An | An | [3n-1] | n | (n + 1)! | n-simplex | |
| BCn | Cn | [4,3n-2] | n | 2n n! | n-hypercube / n-cross-polytope | |
| Dn | Bn | [3n-3,1,1] | n | 2n−1 n! | n-demihypercube | |
| E6 | E6 | [32,2,1] | 6 | 72x6! = 51840 | 221, 122 | |
| E7 | E7 | [33,2,1] | 7 | 72x8! = 2903040 | 321, 231, 132 | |
| E8 | E8 | [34,2,1] | 8 | 192x10! = 696729600 | 421, 241, 142 | |
| F4 | F4 | [3,4,3] | 4 | 1152 | 24-cell | |
| G2 | - | [6] | 2 | 12 | hexagon | |
| H2 | G2 | [5] | 2 | 10 | pentagon | |
| H3 | G3 | [3,5] | 3 | 120 | icosahedron / dodecahedron | |
| H4 | G4 | [3,3,5] | 4 | 14400 | 120-cell / 600-cell | |
| I2(p) | D2p | [p] | 2 | 2p | p-gon | |
Symmetry groups of regular polytopes
All symmetry groups of regular polytopes are finite Coxeter groups. Note that dual polytopes have the same symmetry group.
There are three series of regular polytopes in all dimensions. The symmetry group of a regular n-simplex is the symmetric group Sn+1, also known as the Coxeter group of type An. The symmetry group of the n-cube and its dual, the n-cross-polytope, is BCn, and is known as the hyperoctahedral group.
The exceptional regular polytopes in dimensions two, three, and four, correspond to other Coxeter groups. In two dimensions, the dihedral groups, which are the symmetry groups of regular polygons, form the series I2(p). In three dimensions, the symmetry group of the regular dodecahedron and its dual, the regular icosahedron, is H3, known as the full icosahedral group. In four dimensions, there are three special regular polytopes, the 24-cell, the 120-cell, and the 600-cell. The first has symmetry group F4, while the other two are dual and have symmetry group H4.
The Coxeter groups of type Dn, E6, E7, and E8 are the symmetry groups of certain semiregular polytopes.
| Family n |
n-simplex | n-hypercube | n-orthoplex | n-demicube | 1k2 | 2k1 | k21 | pentagonal polytope | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Group | An | BCn |
|
|
Hn | |||||||||||
| 2 |  (Triangle) |
 Square |
p-gon |
 Hexagon |
 Pentagon | |||||||||||
| 3 |  Tetrahedron |
 Cube |
 Octahedron |
 Tetrahedron |
 Dodecahedron |
 Icosahedron | ||||||||||
| 4 |  5-cell |
 |
 16-cell |
 Demitesseract |
 24-cell |
 120-cell |
 600-cell | |||||||||
| 5 |  5-simplex |
 5-cube |
 5-orthoplex |
 5-demicube |
||||||||||||
| 6 |  6-simplex |
 6-cube |
 6-orthoplex |
 6-demicube |
 122 |
 221 |
||||||||||
| 7 |  7-simplex |
 7-cube |
 7-orthoplex |
 7-demicube |
 132 |
 231 |
 321 |
|||||||||
| 8 |  8-simplex |
 8-cube |
 8-orthoplex |
 8-demicube |
 142 |
 241 |
 421 |
|||||||||
| 9 |  9-simplex |
 9-cube |
 9-orthoplex |
 9-demicube |
||||||||||||
| 10 |  10-simplex |
 10-cube |
 10-orthoplex |
 10-demicube |
||||||||||||
| Fundamental convex regular and uniform polytopes in dimensions 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | BCn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform polychoron | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes | ||||||||||||
Affine Coxeter groups

The affine Coxeter groups form a second important series of Coxeter groups. These are not finite themselves, but each contains a normal abelian subgroup such that the corresponding quotient group is finite. In each case, the quotient group is itself a Coxeter group, and the Coxeter graph is obtained from the Coxeter graph of the Coxeter group by adding an additional vertex and one or two additional edges. For example, for n ≥ 2, the graph consisting of n+1 vertices in a circle is obtained from An in this way, and the corresponding Coxeter group is the affine Weyl group of An. For n = 2, this can be pictured as the symmetry group of the standard tiling of the plane by equilateral triangles.
A list of the affine Coxeter groups follows:
| Group symbol | Witt symbol | Bracket notation | Related uniform tessellation(s) | Coxeter-Dynkin diagram |
|---|---|---|---|---|
 |
Pn+1 | [3[n]] | Simplectic honeycomb | or |
 |
Sn+1 | [4,3n-3,31,1] | Demihypercubic honeycomb | |
 |
Rn+1 | [4,3n-2,4] | Hypercubic honeycomb | |
 |
Qn+1 | [ 31,1,3n-4,31,1] | Demihypercubic honeycomb | |
 |
T7 | [32,2,2] | 222 | |
 |
T8 | [33,3,1] | 331, 133 | |
 |
T9 | [35,2,1] | 521, 251, 152 | |
 |
U5 | [3,4,3,3] | 16-cell honeycomb 24-cell honeycomb | |
 |
V3 | [6,3] | Hexagonal tiling and Triangular tiling | |
 |
W2 | [∞] | apeirogon | |
The subscript is one less than the number of nodes in each case, since each of these groups was obtained by adding a node to a finite group's graph.
Hyperbolic Coxeter groups
There are infinitely many hyperbolic Coxeter groups describing reflection groups in hyperbolic space, notably including the hyperbolic triangle groups.
Partial orders
A choice of reflection generators gives rise to a length function l on a Coxeter group, namely the minimum number of uses of generators required to express a group element; this is precisely the length in the word metric in the Cayley graph. An expression for v using l(v) generators is a reduced word. For example, the permutation (13) in S3 has two reduced words, (12)(23)(12) and (23)(12)(23). The function  defines a map
defines a map 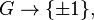 generalizing the sign map for the symmetric group.
generalizing the sign map for the symmetric group.
Using reduced words one may define three partial orders on the Coxeter group, the (right) weak order, the absolute order and the Bruhat order (named for François Bruhat). An element v exceeds an element u in the Bruhat order if some (or equivalently, any) reduced word for v contains a reduced word for u as a substring, where some letters (in any position) are dropped. In the weak order, v ≥ u if some reduced word for v contains a reduced word for u as an initial segment. Indeed, the word length makes this into a graded poset. The Hasse diagrams corresponding to these orders are objects of study, and are related to the Cayley graph determined by the generators. The absolute order is defined analogously to the weak order, but with generating set/alphabet consisting of all conjugates of the Coxeter generators.
For example, the permutation (1 2 3) in S3 has only one reduced word, (12)(23), so covers (12) and (23) in the Bruhat order but only covers (12) in the weak order.
Homology
Since a Coxeter group W is generated by finitely many elements of order 2, its abelianization is an elementary abelian 2-group, i.e. it is isomorphic to the direct sum of several copies of the cyclic group Z2. This may be restated in terms of the first homology group of W.
The Schur multiplier M(W) (related to the second homology) was computed in (Ihara & Yokonuma 1965) for finite reflection groups and in (Yokonuma 1965) for affine reflection groups, with a more unified account given in (Howlett 1988). In all cases, the Schur multiplier is also an elementary abelian 2-group. For each infinite family {Wn} of finite or affine Weyl groups, the rank of M(W) stabilizes as n goes to infinity.
See also
- Artin group
- Triangle group
- Coxeter element
- Coxeter number
- Complex reflection group
- Chevalley–Shephard–Todd theorem
- Hecke algebra, a quantum deformation of the group algebra
- Kazhdan–Lusztig polynomial
- Longest element of a Coxeter group
- Supersoluble arrangement
References
Further reading
- Coxeter, H.S.M. (1934), "Discrete groups generated by reflections", Ann. Of Math. 35 (3): 588–621, doi:10.2307/1968753, JSTOR 1968753
- Coxeter, H.S.M. (1935), "The complete enumeration of finite groups of the form
 ", J. London Math. Soc. 10: 21–25
", J. London Math. Soc. 10: 21–25 - Davis, Michael W. (2007), The Geometry and Topology of Coxeter Groups, ISBN 978-0-691-13138-2
- Larry C Grove and Clark T. Benson, Finite Reflection Groups, Graduate texts in mathematics, vol. 99, Springer, (1985)
- James E. Humphreys, Reflection Groups and Coxeter Groups, Cambridge studies in advanced mathematics, 29 (1990)
- Richard Kane, Reflection Groups and Invariant Theory, CMS Books in Mathematics, Springer (2001)
- Anders Björner and Francesco Brenti, Combinatorics of Coxeter Groups, Graduate Texts in Mathematics, vol. 231, Springer, (2005)
- Howard Hiller, Geometry of Coxeter groups. Research Notes in Mathematics, 54. Pitman (Advanced Publishing Program), Boston, Mass.-London, 1982. iv+213 pp. ISBN 0-273-08517-4
- Nicolas Bourbaki, Lie Groups and Lie Algebras: Chapter 4-6, Elements of Mathematics, Springer (2002). ISBN 978-3-540-42650-9
- Howlett, Robert B. (1988), "On the Schur Multipliers of Coxeter Groups", Journal of the London Mathematical Society, 2 38 (2): 263–276, doi:10.1112/jlms/s2-38.2.263
- Vinberg, E. B. (1984), "Absence of crystallographic groups of reflections in Lobachevski spaces of large dimension", Trudy Moskov. Mat. Obshch. 47
- Ihara, S.; Yokonuma, Takeo (1965), "On the second cohomology groups (Schur-multipliers) of finite reflection groups", Jour. Fac. Sci. Univ. Tokyo, Sect. 1 11: 155–171
- Yokonuma, Takeo (1965), "On the second cohomology groups (Schur-multipliers) of infinite discrete reflection groups", Jour. Fac. Sci. Univ. Tokyo, Sect. 1 11: 173–186
External links
- Hazewinkel, Michiel, ed. (2001), "Coxeter group", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Weisstein, Eric W., "Coxeter group", MathWorld.
- Jenn software for visualizing the Cayley graphs of finite Coxeter groups on up to four generators
