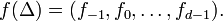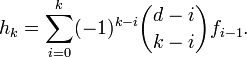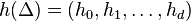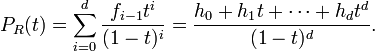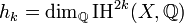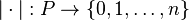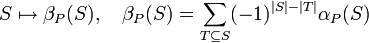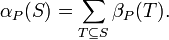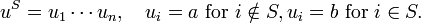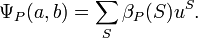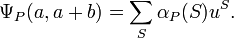H-vector

From Wikipedia, the free encyclopedia

In algebraic combinatorics, the h-vector of a simplicial polytope is a fundamental invariant of the polytope which encodes the number of faces of different dimensions and allows one to express the Dehn–Sommerville equations in a particularly simple form. A characterization of the set of h-vectors of simplicial polytopes was conjectured by Peter McMullen and proved by Lou Billera and Carl W. Lee and Richard Stanley (g-theorem). The definition of h-vector applies to arbitrary abstract simplicial complexes. The g-conjecture states that for simplicial spheres, all possible h-vectors occur already among the h-vectors of the boundaries of convex simplicial polytopes.

Stanley introduced a generalization of the h-vector, the toric h-vector, which is defined for an arbitrary ranked poset, and proved that for the class of Eulerian posets, the Dehn–Sommerville equations continue to hold. A different, more combinatorial, generalization of the h-vector that has been extensively studied is the flag h-vector of a ranked poset. For Eulerian posets, it can be more concisely expressed by means of a noncommutative polynomial in two variables called the cd-index.

Definition

Let Δ be an abstract simplicial complex of dimension d − 1 with f_i i-dimensional faces and f₋₁ = 1. These numbers are arranged into the f-vector of Δ,

$f(\Delta )=(f_{{-1}},f_{0},\ldots ,f_{{d-1}}).$

An important special case occurs when Δ is the boundary of a d-dimensional convex polytope.

For k = 0, 1, …, d, let

$h_{k}=\sum _{{i=0}}^{k}(-1)^{{k-i}}{\binom {d-i}{k-i}}f_{{i-1}}.$

The tuple

$h(\Delta )=(h_{0},h_{1},\ldots ,h_{d})$

is called the h-vector of Δ. The f-vector and the h-vector uniquely determine each other through the linear relation

$\sum _{{i=0}}^{{d}}f_{{i-1}}(t-1)^{{d-i}}=\sum _{{k=0}}^{{d}}h_{{k}}t^{{d-k}}.$

Let R = k[Δ] be the Stanley–Reisner ring of Δ. Then its Hilbert–Poincaré series can be expressed as

$P_{{R}}(t)=\sum _{{i=0}}^{{d}}{\frac {f_{{i-1}}t^{i}}{(1-t)^{{i}}}}={\frac {h_{0}+h_{1}t+\cdots +h_{d}t^{d}}{(1-t)^{d}}}.$

This motivates the definition of the h-vector of a finitely generated positively graded algebra of Krull dimension d as the numerator of its Hilbert–Poincaré series written with the denominator (1 − t)^d.

Toric h-vector

To an arbitrary graded poset P, Stanley associated a pair of polynomials f(P,x) and g(P,x). Their definition is recursive in terms of the polynomials associated to intervals [0,y] for all y ∈ P, y ≠ 1, viewed as ranked posets of lower rank (0 and 1 denote the minimal and the maximal elements of P). The coefficients of f(P,x) form the toric h-vector of P. When P is an Eulerian poset of rank d + 1 such that P − 1 is simplicial, the toric h-vector coincides with the ordinary h-vector constructed using the numbers f_i of elements of P − 1 of given rank i + 1. In this case the toric h-vector of P satisfies the Dehn–Sommerville equations

$h_{k}=h_{{d-k}}.$

The reason for the adjective "toric" is a connection of the toric h-vector with the intersection cohomology of a certain projective toric variety X whenever P is the boundary complex of rational convex polytope. Namely, the components are the dimensions of the even intersection cohomology groups of X:

$h_{k}=\operatorname {dim}_{{{\mathbb {Q}}}}\operatorname {IH}^{{2k}}(X,{\mathbb {Q}})$

(the odd intersection cohomology groups of X are all zero). The Dehn–Sommerville equations are a manifestation of the Poincaré duality in the intersection cohomology of X.

Flag h-vector and cd-index

A different generalization of the notions of f-vector and h-vector of a convex polytope has been extensively studied. Let P be a finite graded poset of rank n − 1, so that each maximal chain in P has length n. For any S, a subset of {1,…,n}, let α_P(S) denote the number of chains in P whose ranks constitute the set S. More formally, let

$|\cdot |:P\to \{0,1,\ldots ,n\}$

be the rank function of P and let P_S be the S-rank selected subposet, which consists of the elements from P whose rank is in S:

$P_{S}=\{x\in P:|x|\in S\}.$

Then α_P(S) is the number of the maximal chains in P(S) and the function

$S\mapsto \alpha _{P}(S)$

is called the flag f-vector of P. The function

$S\mapsto \beta _{P}(S),\quad \beta _{P}(S)=\sum _{{T\subseteq S}}(-1)^{{|S|-|T|}}\alpha _{P}(S)$

is called the flag h-vector of P. By the inclusion–exclusion principle,

$\alpha _{P}(S)=\sum _{{T\subseteq S}}\beta _{P}(T).$

The flag f- and h-vectors of P refine the ordinary f- and h-vectors of its order complex Δ(P):

$f_{{i-1}}(\Delta (P))=\sum _{{|S|=i}}\alpha _{P}(S),\quad h_{{i}}(\Delta (P))=\sum _{{|S|=i}}\beta _{P}(S).$

The flag h-vector of P can be displayed via a polynomial in noncommutative variables a and b. For any subset S of {1,…,n}, define the corresponding monomial in a and b,

$u^{S}=u_{1}\cdots u_{n},\quad u_{i}=a{\text{ for }}i\notin S,u_{i}=b{\text{ for }}i\in S.$

Then the noncommutative generating function for the flag h-vector of P is defined by

$\Psi _{P}(a,b)=\sum _{{S}}\beta _{P}(S)u^{{S}}.$

From the relation between α_P(S) and β_P(S), the noncommutative generating function for the flag f-vector of P is

$\Psi _{P}(a,a+b)=\sum _{{S}}\alpha _{P}(S)u^{{S}}.$

Margaret Bayer and Lou Billera determined the most general linear relations that hold between the components of the flag h-vector of an Eulerian poset P. Fine noted an elegant way to state these relations: there exists a noncommutative polynomial Φ_P(c,d), called the cd-index of P, such that

$\Psi _{P}(a,b)=\Phi _{P}(a+b,ab+ba).$

Stanley proved that all coefficients of the cd-index of the boundary complex of a convex polytope are non-negative. He conjectured that this positivity phenomenon persists for a more general class of Eulerian posets that Stanley calls Gorenstein* complexes and which includes simplicial spheres and complete fans. This conjecture was proved by Kalle Karu. The combinatorial meaning of these non-negative coefficients (an answer to the question "what do they count?") remains unclear.

References

Karu, Kalle (2006), "The cd-index of fans and posets", Compositio Math. 142: 701–718, doi:10.1112/S0010437X06001928 .
Stanley, Richard (1996), Combinatorics and commutative algebra, Progress in Mathematics 41 (2nd ed.), Boston, MA: Birkhäuser Boston, Inc., ISBN 0-8176-3836-9 .
Stanley, Richard (1997), Enumerative Combinatorics 1, Cambridge University Press, ISBN 0-521-55309-1 .

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.