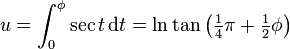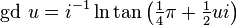Gudermannian function

From Wikipedia, the free encyclopedia
Gudermannian function with its asymptotes y = ±π/2 marked in blue

The Gudermannian function, named after Christoph Gudermann (1798–1852), relates the circular functions and hyperbolic functions without using complex numbers.

It is defined by

{\begin{aligned}{{\rm {{gd}}}}\,x&=\int _{0}^{x}{\frac {{\mathrm {d}}t}{\cosh t}}\\[8pt]&=\arcsin \left(\tanh x\right)={\mathrm {arctan}}\left(\sinh x\right)\\[8pt]&=2\arctan \left[\tanh \left({\tfrac 12}x\right)\right]=2\arctan(e^{x})-{\tfrac 12}\pi .\end{aligned}}\,\!

Some related formulas don't quite work as definitions. For example, for real x, \arccos {\mathrm {sech}}\,x=\vert {\mathrm {gd}}\,x\vert =\operatorname{arcsec}(\cosh x). (See inverse trigonometric functions.)

The following identities hold:

{\begin{aligned}{\color {white}{\dot {{\color {black}\sin {\mathrm {gd}}\,x}}}}&=\tanh x;\quad \csc {\mathrm {gd}}\,x=\coth x;\\\cos {\mathrm {gd}}\,x&={\mathrm {sech}}\,x;\quad \,\sec {\mathrm {gd}}\,x=\cosh x;\\\tan {\mathrm {gd}}\,x&=\sinh x;\quad \,\cot {\mathrm {gd}}\,x={\mathrm {csch}}\,x;\\{}_{{\color {white}.}}\tan {\tfrac {1}{2}}{\mathrm {gd}}\,x&=\tanh {\tfrac {1}{2}}x.\end{aligned}}\,\!
The inverse Gudermannian function

The inverse Gudermannian function, which is defined on the interval −π/2 < x < π/2, is given by

{\begin{aligned}\operatorname {gd}^{{-1}}\,x&=\int _{0}^{x}{\frac {{\mathrm {d}}t}{\cos t}}\\[8pt]&=\ln \left|{\frac {1+\sin x}{\cos x}}\right|={\tfrac 12}\ln \left|{\frac {1+\sin x}{1-\sin x}}\right|\\[8pt]&=\ln \left|\tan x+\sec x\right|=\ln \left|\tan \left({\tfrac 14}\pi +{\tfrac 12}x\right)\right|\\[8pt]&={\mathrm {artanh}}\,(\sin x)={\mathrm {arsinh}}\,(\tan x).\end{aligned}}

(See inverse hyperbolic functions.)

The derivatives of the Gudermannian and its inverse are

{\frac {{\mathrm {d}}}{{\mathrm {d}}x}}\;{\mathrm {gd}}\,x={\mathrm {sech}}\,x;\quad {\frac {{\mathrm {d}}}{{\mathrm {d}}x}}\;\operatorname {gd}^{{-1}}\,x=\sec x.

The expression

{\tfrac {1}{2}}\pi -{\mathrm {gd}}\,x

defines the angle of parallelism function in hyperbolic geometry.

History

The function was introduced by Johann Heinrich Lambert in the 1760s at the same time as the hyperbolic functions. He called it the "transcendent angle," and it went by various names until 1862 when Arthur Cayley suggested it be given its current name as a tribute to Gudermann's work in the 1830s on the theory of special functions.[1] Gudermann had published articles in Crelle's Journal that were collected in Theorie der potenzial- oder cyklisch-hyperbolischen functionen (1833), a book which expounded sinh and cosh to a wide audience (under the guises of {\mathfrak {Sin}} and {\mathfrak {Cos}}).

The notation gd first appears on page 19 of the Philosophical Magazine, vol. XXIV, where Cayley starts by calling gd. u the inverse of the integral of the secant function:

u=\int _{0}^{\phi }\sec t\,{\mathrm {d}}t=\ln \tan \left({\tfrac 14}\pi +{\tfrac 12}\phi \right)

and then derives "the definition" of the transcendent:

\operatorname {gd}\,u=i^{{-1}}\ln \tan \left({\tfrac 14}\pi +{\tfrac 12}ui\right)

observing immediately that it is a real function of u.

Applications

The Gudermannian of the latitudinal (due North/South) distance from the equator on a Mercator projection is the meridian arc length, i.e. actual latitude on the globe.

The Gudermannian appears in a non-periodic solution of the inverted pendulum.[2]

See also

Notes

  1. ↑ George F. Becker, C. E. Van Orstrand. Hyperbolic functions. Read Books, 1931. Page xlix.
  2. ↑ John S. Robertson, "Gudermann and the Simple Pendulum", The College Mathematics Journal 28:4:271–276 (September 1997) at JSTOR

References

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.