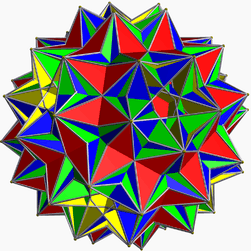
Great disnub dirhombidodecahedron
| Great disnub dirhombidodecahedron | |
|---|---|
 | |
| Type | Uniform star polyhedron |
| Elements | F = 204, E = 240 V = 60 (χ = 32) |
| Faces by sides | 120{3}+60{4}+24{5/2} |
| Wythoff symbol(s) | | (3/2) 5/3 (3) 5/2 |
| Symmetry group | Ih, [5,3], *532 |
| Index references | U-, C-, W- |
| Bowers acronym | Gidisdrid |
 (5/2.4.3.3.3.4. 5/3.4.3/2.3/2.3/2.4)/2 (Vertex figure) |
 Great disnub dirhombidodecacron (dual polyhedron) |
In geometry, the great disnub dirhombidodecahedron, also called Skilling's figure, is a uniform star polyhedron.
It was proven in 1970 that there are only 75 uniform polyhedra other than the infinite families of prisms and antiprisms. John Skilling discovered one more, by relaxing the condition that only two faces may meet at an edge. Some authors do not count it as a uniform polyhedron, because some pairs of edges coincide.
It has 120 edges with 2 faces and 120 edges with 4 faces. If the 4-face edges are counted twice, as two topologically disjoint edges, this figure can be considered to have 360 total edges, and the Euler characteristic becomes -88.
The vertex figure has 4 square faces passing through the center of the model.
Related polyhedra
It shares the same edge arrangement as the great dirhombicosidodecahedron, but has a different set of triangular faces. The vertices and edges are also shared with the uniform compounds of 20 octahedra or 20 tetrahemihexahedra. 180 of the edges are shared with the great snub dodecicosidodecahedron.
 Convex hull |
 Great snub dodecicosidodecahedron |
 Great dirhombicosidodecahedron |
 Great disnub dirhombidodecahedron |
 Compound of twenty octahedra |
 Compound of twenty tetrahemihexahedra |
Dual polyhedron

The dual of the great disnub dirhombidodecahedron is called a great disnub dirhombidodecacron. It is a nonconvex infinite isohedral polyhedron.
Like the visually identical great dirhombicosidodecacron in Magnus Wenninger's Dual Models, it is represented with intersecting infinite prisms passing through the model center, cut off at a certain point that is convenient for the maker. Wenninger suggested these figures are members of a new class of stellation polyhedra, called stellation to infinity. However, he also acknowledged that strictly speaking they are not polyhedra because their construction does not conform to the usual definitions.
Filling
There is some controversy on how to colour the faces of this polyhedron. Although the common way to fill in a polygon is to just colour its whole interior, this can result in some filled regions hanging as membranes over empty space. Hence, the "neo filling" is sometimes used instead as a more accurate filling. In the neo filling, orientable polyhedra are filled traditionally, but non-orientable polyhedra have their faces filled with the modulo-2 method (only odd-density regions are filled in). In addition, overlapping regions of coplanar faces can cancel each other out.[1]
 Traditional filling |
 "Neo filling" |
See also
References
- Skilling, John (1975), "The complete set of uniform polyhedra", Philosophical Transactions of the Royal Society A 278 (1278): 111–135, doi:10.1098/rsta.1975.0022.
- Weisstein, Eric W., "Great dirhombicosidodecahedron", MathWorld.
- http://www.software3d.com/MillersMonster.php
External links
- http://www.orchidpalms.com/polyhedra/uniform/skilling.htm
- http://www.georgehart.com/virtual-polyhedra/great_disnub_dirhombidodecahedron.html