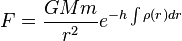Gravitational shielding

From Wikipedia, the free encyclopedia

The term gravitational shielding refers to a hypothetical process of shielding an object from the influence of a gravitational field. Such processes, if they existed, would have the effect of reducing the weight of an object. The shape of the shielded region would be similar to a shadow from the gravitational shield. For example, the shape of the shielded region above a disk would be conical. The height of the cone's apex above the disk would vary directly with the height of the shielding disk above the earth.[1] Experimental evidence to date indicates that no such effect exists. Gravitational shielding is considered to be a violation of the equivalence principle and therefore inconsistent with both Newtonian theory and general relativity.[2]

Tests of the equivalence principle

As of 2008, no experiment was successful in detecting positive shielding results. To quantify the amount of shielding, Quirino Majorana[3] suggested an extinction coefficient h that modifies Newton’s gravitational force law as follows:

F={\frac {GMm}{r^{2}}}e^{{-h\int \rho (r)dr}}

The best laboratory measurements have established an upper bound limit for shielding of 4.3×10−15 m²/kg.[4] Another recent analysis suggested a lower bound of 0.6×10−15.[5] The best estimate based on the most accurate gravity anomaly data during the 1997 solar eclipse has provided a new constraint on the shielding parameter 6×10−19 m²/kg.[6] However, astronomical observations impose much more stringent limits. Based on lunar observations available in 1908, Poincaré[7] established that h can be no greater than 10−18 m²/kg. Subsequently this bound has been greatly improved. Eckhardt[8] showed that lunar ranging data implies an upper bound of 10−22 m²/kg, and Williams, et al.,[9] have improved this to h = (3 ± 5)×10−22 m²/kg. Note that the value is smaller than the uncertainty. The consequence of the negative results of those experiments (which are in good agreement with the predictions of general relativity) is, that every theory which contains shielding effects like Le Sage's theory of gravitation, must reduce those effects to an undetectable level. For a review of the current experimental limits on possible gravitational shielding, see the survey article by Bertolami, et al.[2] Also, for a discussion of recent observations during solar eclipses, see the paper by Unnikrishnan et al.[10]

Majorana's experiments and Russell's criticism

Some shielding experiments were conducted in the early 20th century by Majorana.[3][11] Majorana claimed to have measured positive shielding effects. Henry Norris Russell's analysis of the tidal forces showed that Majorana's positive results had nothing to do with gravitational shielding.[12] To bring Majorana's experiments in accordance with the equivalence principle of General Relativity he proposed a model, in which the mass of a body is diminished by the proximity of another body, but he denied any connection between gravitational shielding and his proposal of mass variation. For another explanation of Majorana's experiments, see Coïsson et al.[13] But Majorana's results couldn't be confirmed up to this day (see the section above) and Russell's mass variation theory, although meant as a modification of general relativity, is inconsistent with standard physics as well.

For a historical review of efforts to detect any effects of gravitational shielding in the early 20th century, see the article by Martins.[14]

Minority views

The consensus view of the scientific community is that gravitational shielding does not exist, but there have been occasional investigations into this topic, such the 1999 NASA-funded paper by Li, et al.[15][16][17] See also the writings of the Russian engineer, Eugene Podkletnov.[18] While experimenting with rotating superconductors he noticed that pipe smoke from a nearby researcher appeared to be collecting in a column above his apparatus. He then devised an experiment in which he magnetically levitated a superconducting rotating disc, and he reported that objects held above the rotating disc underwent a reduction of between 0.5 to 2% in weight. Analyses of Podkletnov's observations by Giovanni Modanese[19] and Ning Wu[20] indicated various applications of quantum gravity theory could allow gravitational shielding phenomena. Podkletnov's findings have yet to be replicated or verified through independent experimental data.

References

  1. ↑ Unnikrishan, C. S. (1996). Does a superconductor shield gravity? Physica C, 266, 133-137.
  2. ↑ 2.0 2.1 Bertolami, O. & Paramos, J. & Turyshev, S. G. (2006), General Theory of Relativity: Will it survive the next decade?, in H. Dittus, C. Laemmerzahl, S. Turyshev, Lasers, Clocks, and Drag-Free: Technologies for Future Exploration in Space and Tests of Gravity: 27-67
  3. ↑ 3.0 3.1 Majorana, Q., (1920). “On gravitation. Theoretical and experimental researches”, Phil. Mag. [ser. 6] 39, 488-504.
  4. ↑ Unnikrishnan and Gillies (2000), Phys Rev D, 61
  5. ↑ Caputo M., On new limits of the coefficient of gravitation shielding,J. Astrophysics and Astronomy,vol. 27, 439-441 (2006).
  6. ↑ Yang X.-S., Wang Q.-S., Gravity Anomaly During the Mohe Total Solar Eclipse and New Constraint on Gravitational Shielding Parameter,Astrophysics and Space Science, Vol.282, 245-253 (2002).
  7. ↑ Poincaré, H. (1908). "La dynamique de l'électron", Revue générale des sciences pures et appliquées 19, pp. 386-402, reprinted in Science and Method. Flammarion, Paris. An English translation was published as Foundation of Science, Science Press, New York, 1929.
  8. ↑ D. H. Eckhardt, Phy Rev D, 42, 1990, 2144
  9. ↑ Williams, et al., “Testing the Equivalence Principle on the Ground and in Space”, (2006), to be published by Springer Verlag, Lecture Notes in Physics, gr-qc/0507083
  10. ↑ Unnikrishnan, Mohapatra, Gillies (2002), “Anomalous gravity data during the 1997 total solar eclipse do not support the hypothesis of gravitational shielding”, Physical Review D, vol 63, available online at http://www.astro.oma.be/ICET/bim/bim138/vanruymbeke2.htm
  11. ↑ Martins, R. A., 2002. "Majorana’s experiments on gravitational absorption", in: Pushing Gravity: New Perspectives on Le Sage's Theory of Gravitation (ed. Edwards, M. R.), Apeiron, Montreal, pp. 219-238.
  12. ↑ Russell, H.N. (1921). “On Majorana’s theory of gravitation”. Astrophys. J. 54, 334-346.
  13. ↑ Coïsson, R.; Mambriani, G.; Podini, P. "A new interpretation of Quirino Majorana's experiments on gravitation and a proposal for testing his results", Il Nuovo Cimento B, vol. 117, Issue 04, p.469.
  14. ↑ Martins, R. A., 1999. “The search for gravitational absorption in the early 20th century”, in: The Expanding Worlds of General Relativity (Einstein Studies, vol. 7) (eds., Goemmer, H., Renn, J., and Ritter, J.), Birkhäuser, Boston, pp. 3-44.
  15. ↑
    • N. Li, D. Noever, T. Robertson, R. Koczor and W. Brantley, Static Test for a Gravitational Force Coupled to Type II YBCO Superconductors, Physica C 281, 260-267
  16. ↑ R. Koczor and D. Noever, Fabrication of Large Bulk Ceramic Superconductor Disks for Gravity Modification Experiments and Performance of YBCO Disks Under e.m. Field Excitation, NASA Marshall, Huntsville, AL, AIAA 99-2147, 35th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, 20–24 June 1999, Los Angeles, CA.
  17. ↑ Space.com on NASA funding
  18. ↑
  19. ↑ Modanese, G. (1996, August 20). Theoretical analysis of a reported weak-gravitational-shielding effect. Europhysics Letters, 35(6), 413-418.
  20. ↑ Wu, N. (2004). Gravitational shielding effect in gauge theory of gravity. Communications in Theoretical Physics, 41(4), 567-572.
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.