Graph toughness

From Wikipedia, the free encyclopedia

In this graph, removing the four red vertices would produce four connected components (depicted in four different colours). However, there is no set of k vertices whose removal leaves more than k components. Therefore, its toughness is exactly 1.

In graph theory, toughness is a measure of the connectivity of a graph. A graph $G$ is said to be $t$ -tough for a given real number $t$ if, for every integer $k > 1$ , $G$ cannot be split into $k$ different connected components by the removal of fewer than $tk$ vertices. For instance, a graph is $1$ -tough if the number of components formed by removing a set of vertices is always at most as large as the number of removed vertices. The toughness of a graph is the maximum $t$ for which it is $t$ -tough; this is a finite number for all graphs except the complete graphs, which by convention have infinite toughness.

Graph toughness was first introduced by Václav Chvátal (1973). Since then there has been extensive work by other mathematicians on toughness; the recent survey by Bauer, Broersma & Schmiechel (2006) lists 99 theorems and 162 papers on the subject.

Examples

Removing $k$ vertices from a path graph may split the remaining graph into $k+1$ connected components. The maximum ratio of components to removed vertices is achieved by removing one vertex (from the middle of the path) and splitting it into two components. Therefore, paths are ${\frac 12}$ -tough. In contrast, removing $k$ vertices from a cycle graph leaves at most $k$ remaining connected components, so the cycle is $1$ -tough.

Connection to vertex connectivity

If a graph is 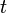$t$ -tough, then one consequence (obtained by setting $k=2$ ) is that any set of $2t-1$ nodes can be removed without splitting the graph in two. That is, every 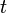$t$ -tough graph is also $2t$ .

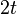Connection to Hamiltonicity

Chvátal (1973) observed that every cycle, and therefore every Hamiltonian graph, is $1$ -tough; that is, being $1$ -tough is a necessary condition for a graph to be Hamiltonian. He conjectured that the connection between toughness and Hamiltonicity goes in both directions: that there exists a threshold 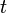$t$ such that every 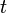$t$ -tough graph is Hamiltonian. Chvátal's original conjecture that $t=2$ would have proven Fleischner's theorem but was disproved by Bauer, Broersma & Veldman (2000) The existence of a larger toughness threshold for Hamiltonicity remains open.

References

Bauer, Douglas; Broersma, Hajo; Schmeichel, Edward (2006), "Toughness in graphs—a survey", Graphs and Combinatorics 22 (1): 1–35, doi:10.1007/s00373-006-0649-0, MR 2221006 .
Bauer, D.; Broersma, H. J.; Veldman, H. J. (2000), Not every 2-tough graph is Hamiltonian, "Proceedings of the 5th Twente Workshop on Graphs and Combinatorial Optimization (Enschede, 1997)", Discrete Applied Mathematics (1-3 ed.) 99: 317–321, doi:10.1016/S0166-218X(99)00141-9, MR 1743840 .
Chvátal, Václav (1973), "Tough graphs and Hamiltonian circuits", Discrete Mathematics 5 (3): 215–228, doi:10.1016/0012-365X(73)90138-6, MR 0316301 .

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.