Graph bandwidth
In graph theory, the graph bandwidth problem is to label the n vertices vi of a graph G with distinct integers f(vi) so that the quantity  is minimized (E is the edge set of G).[1]
The problem may be visualized as placing the vertices of a graph at distinct integer points along the x-axis so that the length of the longest edge is minimized. Such placement is called linear graph arrangement, linear graph layout or linear graph placement.[2]
is minimized (E is the edge set of G).[1]
The problem may be visualized as placing the vertices of a graph at distinct integer points along the x-axis so that the length of the longest edge is minimized. Such placement is called linear graph arrangement, linear graph layout or linear graph placement.[2]
The weighted graph bandwidth problem is a generalization wherein the edges are assigned weights wij and the cost function to be minimized is  .
.
In terms of matrices, the (unweighted) graph bandwidth is the bandwidth of the symmetric matrix which is the adjacency matrix of the graph.
Bandwidth formulas for some graphs
For several families of graphs, the bandwidth  is given by an explicit formula.
is given by an explicit formula.
The bandwidth of a path graph 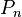 on n vertices is
on n vertices is  , and for a complete graph
, and for a complete graph 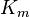 we have
we have  . For the complete bipartite graph
. For the complete bipartite graph 
 , assuming
, assuming  ,
,
which was proved by Chvátal.[3] As a special case of this formula, the star graph  on k+1 vertices has bandwidth
on k+1 vertices has bandwidth  .
.
For the hypercube graph  on
on  vertices the bandwidth was determined by Harper (1966) to be
vertices the bandwidth was determined by Harper (1966) to be
Chvatálová showed[4] that the bandwidth of the 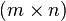 square grid graph
square grid graph 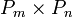 , that is, the Cartesian product of two path graphs on
, that is, the Cartesian product of two path graphs on  and
and  vertices, is equal to
vertices, is equal to 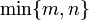 .
.
Bounds
The bandwidth of a graph can be bounded in terms of various other graph parameters. For instance, letting χ(G) denote the chromatic number of G,
- φ(G) ≥ χ(G)-1;
letting diam(G) denote the diameter of G, the following inequalities hold:[5]
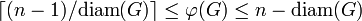 ,
,
where  is the number of vertices in
is the number of vertices in  .
.
If a graph  has bandwidth
has bandwidth  , then its pathwidth is at most
, then its pathwidth is at most  (Kaplan & Shamir 1996), and its tree-depth is at most
(Kaplan & Shamir 1996), and its tree-depth is at most  (Gruber 2012). In contrast, as noted in the previous section, the star graph
(Gruber 2012). In contrast, as noted in the previous section, the star graph 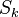 , a structurally
very simple example of a tree, has comparatively large bandwidth. Observe that the pathwidth of
, a structurally
very simple example of a tree, has comparatively large bandwidth. Observe that the pathwidth of 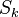 is 1, and its tree-depth is 2.
is 1, and its tree-depth is 2.
Some graph families of bounded degree have sublinear bandwidth: Chung (1988) proved that if T is a tree of maximum degree at most ∆, then
 .
.
More generally, for planar graphs of bounded maximum degree at most ∆, a similar bound holds (cf. Böttcher et al. 2010):
 .
.
Computing the bandwidth
Both the unweighted and weighted versions are special cases of the quadratic bottleneck assignment problem. The bandwidth problem is NP-hard, even for some special cases.[6] Regarding the existence of efficient approximation algorithms, it is known that the bandwidth is NP-hard to approximate within any constant, and this even holds when the input graphs are restricted to caterpillar trees (Dubey, Feige & Unger 2010). On the other hand, a number of polynomially-solvable special cases are known.[2] A heuristic algorithm for obtaining linear graph layouts of low bandwidth is the Cuthill–McKee algorithm.
Applications
The interest in this problem comes from some application areas.
One area is sparse matrix/band matrix handling, and general algorithms from this area, such as Cuthill–McKee algorithm, may be applied to find approximate solutions for the graph bandwidth problem.
Another application domain is in electronic design automation. In standard cell design methodology, typically standard cells have the same height, and their placement is arranged in a number of rows. In this context, graph bandwidth problem models the problem of placement of a set of standard cells in a singe row with the goal of minimizing the maximal propagation delay (which is assumed to be proportional to wire length).
See also
- Pathwidth, a different NP-complete optimization problem involving linear layouts of graphs.
References
- ↑ (Chinn et al. 1982)
- ↑ 2.0 2.1 "Coping with the NP-Hardness of the Graph Bandwidth Problem", Uriel Feige, Lecture Notes in Computer Science, Volume 1851, 2000, pp. 129-145, doi:10.1007/3-540-44985-X_2
- ↑ A remark on a problem of Harary. V. Chvátal, Czechoslovak Mathematical Journal 20(1):109–111, 1970. http://dml.cz/dmlcz/100949
- ↑ Optimal Labelling of a product of two paths. J. Chvatálová, Discrete Mathematics 11, 249–253, 1975.
- ↑ Chinn et al. 1982
- ↑ Garey–Johnson: GT40
- Böttcher, J.; Pruessmann, K. P.; Taraz, A.; Würfl, A. (2010). "Bandwidth, expansion, treewidth, separators and universality for bounded-degree graphs". European Journal of Combinatorics 31: 1217–1227. doi:10.1016/j.ejc.2009.10.010.
- Chinn, P. Z.; Chvátalová, J.; Dewdney, A. K.; Gibbs, N. E. (1982). "The bandwidth problem for graphs and matrices—a survey". Journal of Graph Theory 6: 223–254. doi:10.1002/jgt.3190060302.
- Chung, Fan R. K. (1988), "Labelings of Graphs", Selected Topics in Graph Theory, Academic Press, pp. 151–168, ISBN 978-0-12-086203-0
- Dubey, C.; Feige, U.; Unger, W. (2010). "Hardness results for approximating the bandwidth". Journal of Computer and System Sciences 77: 62–90. doi:10.1016/j.jcss.2010.06.006.
- Garey, M.R.; Johnson, D.S. (1979). Computers and Intractability: A Guide to the Theory of NP-Completeness. New York: W.H. Freeman. ISBN 0-7167-1045-5.
- Gruber, Hermann (2012), "On Balanced Separators, Treewidth, and Cycle Rank", Journal of Combinatorics 3 (4): 669–682
- Harper, L. (1966). "Optimal numberings and isoperimetric problems on graphs". Journal of Combinatorial Theory 1: 385–393. doi:10.1016/S0021-9800(66)80059-5.
- Kaplan, Haim; Shamir, Ron (1996), "Pathwidth, bandwidth, and completion problems to proper interval graphs with small cliques", SIAM Journal on Computing 25: 540–561
External links
- Minimum bandwidth problem, in: Pierluigi Crescenzi and Viggo Kann (eds.), A compendium of NP optimization problems. Accessed May 26, 2010.
