Gradient-related

From Wikipedia, the free encyclopedia

Gradient-related is a term used in multivariable calculus to describe a direction. A direction sequence 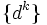$\{d^{k}\}$ is gradient-related to 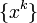$\{x^{k}\}$ if for any subsequence 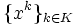$\{x^{k}\}_{{k\in K}}$ that converges to a nonstationary point, the corresponding subsequence 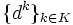$\{d^{k}\}_{{k\in K}}$ is bounded and satisfies

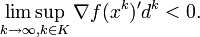
$\limsup _{{k\rightarrow \infty ,k\in K}}\nabla f(x^{k})'d^{k}<0.$

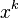A gradient-related direction is usually encountered in the gradient-based iterative optimisation of a function $f$ . At each iteration $k$ the current vector is $x^{k}$ and we move in the direction 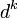$d^{k}$ , thus generating a sequence of directions.

It is easy to guarantee that the directions we generate are gradient-related, by for example setting them equal to the gradient at each point.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.