Graded (mathematics)

From Wikipedia, the free encyclopedia

This disambiguation page lists articles associated with the same title.
If an internal link led you here, you may wish to change the link to point directly to the intended article.

In mathematics, the term “graded” has a number of related meanings:

An algebraic structure is said to be I-graded for an index set I if it has a gradation or grading, i.e. a decomposition into a direct sum of structures; the elements of are said to be “homogenous of degree i”.
- The index set I is most commonly ${\mathbb {N}}$ or ${\mathbb {Z}}$ , and may be required to have extra structure depending on the type of $X$ .
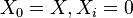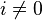- The trivial ( ${\mathbb {Z}}$ - or ${\mathbb {N}}$ -) gradation has $X_{0}=X,X_{i}=0$ for $i\neq 0$ and a suitable trivial structure $0$ .
- An algebraic structure is said to be doubly graded if the index set is a direct product; the pairs may be called as “bidegrees” (e.g. see spectral sequence).
A I-graded vector space or graded linear space for a set I is thus a vector space with a decomposition into a direct sum of spaces.
- A graded linear map is a map between graded vector spaces respecting their gradations.
A graded ring is a ring that is a direct sum of abelian groups such that 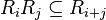, with taken from some monoid, usually or , or semigroup (for a ring without identity).
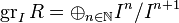- The associated graded ring of a commutative ring $R$ with respect to a proper ideal $I$ is $\operatorname {gr}_{I}R=\oplus _{{n\in {\mathbb {N}}}}I^{n}/I^{{n+1}}$ .
A graded module is left module over a graded ring which is a direct sum 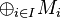of modules satisfying .
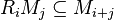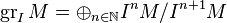- The associated graded module of an $R$ -module $M$ with respect to a proper ideal $I$ is $\operatorname {gr}_{I}M=\oplus _{{n\in {\mathbb {N}}}}I^{n}M/I^{{n+1}}M$ .
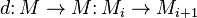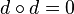- A differential graded module, differential graded ${\mathbb {Z}}$ -module or DG-module is a graded module $M$ with a differential $d\colon M\to M\colon M_{i}\to M_{{i+1}}$ making $M$ a chain complex, i.e. $d\circ d=0$ .
A graded algebra is an algebra over a ring that is graded as a ring; if is graded we also require .
- The graded Leibniz rule for a map 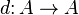$d\colon A\to A$ on a graded algebra $A$ specifies that $d(a\cdot b)=(da)\cdot b+(-1)^{{|a|}}a\cdot (db)$ .
- A differential graded algebra, DG-algebra or DGAlgebra is a graded algebra which is a differential graded module whose differential obeys the graded Leibniz rule.
- A homogeneous derivation on a graded algebra A is a homogeneous linear map of grade d = |D| on A such that 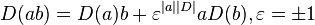$D(ab)=D(a)b+\varepsilon ^{{|a||D|}}aD(b),\varepsilon =\pm 1$ acting on homogeneous elements of A.
- A graded derivation is a sum of homogeneous derivations with the same $\varepsilon$ .
- A DGA is an augmented DG-algebra, or differential graded augmented algebra, (see differential graded algebra).
- A superalgebra is a a Z₂-graded algebra.
  - A graded-commutative superalgebra satisfies the “supercommutative” law 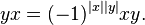$yx=(-1)^{{|x||y|}}xy.\,$ for homogenous x,y, where 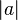$|a|$ represents the “parity” of $a$ , i.e. 0 or 1 depending on the component in which it lies.
- CDGA may refer to the category of augmented differential graded commutative algebras.
A graded Lie algebra is a Lie algebra which is graded as a vector space by a gradation compatible with its Lie bracket.
- A graded Lie superalgebra is a graded Lie algebra with the requirement for anticommutativity of its Lie bracket relaxed.
- A supergraded Lie superalgebra is a graded Lie superalgebra with an additional super Z/2Z-gradation.
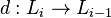- A Differential graded Lie algebra is a graded vector space over a field of characteristic zero together with a bilinear map $[,]:L_{i}\otimes L_{j}\to L_{{i+j}}$ and a differential $d:L_{i}\to L_{{i-1}}$ satisfying $[x,y]=(-1)^{{|x||y|+1}}[y,x],$ for any homogeneous elements x, y in L, the “graded Jacobi identity” and the graded Leibniz rule.
The Graded Brauer group is a synonym for the Brauer–Wall group $BW(F)$ classifying finite-dimensional graded central division algebras over the field F.
An -graded category for a category is a category 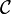together with a functor .
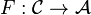- A differential graded category or DG category is a category whose morphism sets form differential graded ${\mathbb {Z}}$ -modules.
Graded manifold – extension of the manifold concept based on ideas coming from supersymmetry and supercommutative algebra, including sections on
- Graded function
- Graded vector fields
- Graded exterior forms
- Graded differential geometry
- Graded differential calculus
Functionally graded elements are elements used in finite element analysis.
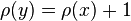A graded poset is a poset $P$ with a rank function $\rho \colon P\to {\mathbb {N}}$ compatible with the ordering (so ρ(x)<ρ(y) ⇐ x < y) such that y covers x ⇒ $\rho (y)=\rho (x)+1$ .

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.