Graceful labeling

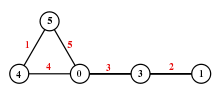
From Wikipedia, the free encyclopedia
A graceful labeling. Vertex labels are in black, edge labels in red

In graph theory, a graceful labeling of a graph with m edges is a labeling of its vertices with some subset of the integers between 0 and m inclusive, such that no two vertices share a label, and such that each edge is uniquely identified by the positive, or absolute difference between its endpoints.[1] A graph which admits a graceful labeling is called a graceful graph.

The name "graceful labeling" is due to Solomon W. Golomb; this class of labelings was originally given the name β-labelings by Alex Rosa in a 1967 paper on graph labelings.[2]

A major unproven conjecture in graph theory is the Ringel–Kotzig conjecture, named after Gerhard Ringel and Anton Kotzig, which hypothesizes that all trees are graceful. The Ringel-Kotzig conjecture is also known as the "graceful labeling conjecture". Kotzig once called the effort to prove the conjecture a "disease".[3]

Selected results

  • In his original paper, Rosa proved that an Eulerian graph with number of edges m ≡ 1 (mod 4) or m ≡ 2 (mod 4) can't be graceful.[2]
  • Also in his original paper, Rosa proved that the cycle Cn is graceful if and only if n ≡ 0 (mod 4) or n ≡ 3 (mod 4).
  • All path graphs and caterpillar graphs are graceful.
  • All lobster graphs with a perfect matching are graceful.[4]
  • All trees with at most 27 vertices are graceful; this result was shown by Aldred and McKay in 1998 using a computer program.[5][6] An extension of this (using a different computational method) up to trees with 35 vertices was claimed in 2010 by the Graceful Tree Verification Project, a distributed computing project led by Wenjie Fang.[7]
  • All wheel graphs, web graphs, Helm graphs, gear graphs, and rectangular grids are graceful.[5]
  • All n-dimensional hypercubes are graceful.[8]
  • All simple graphs with four or fewer vertices are graceful. The only non-graceful simple graphs with five vertices are the 5-cycle (pentagon); the complete graph K5; and the butterfly graph.[9]

See also

References

  1. ↑ Virginia Vassilevska, "Coding and Graceful Labeling of trees." SURF 2001. PostScript
  2. ↑ 2.0 2.1 Rosa, A. (1967), "On certain valuations of the vertices of a graph", Theory of Graphs (Internat. Sympos., Rome, 1966), New York: Gordon and Breach, pp. 349–355, MR 0223271 .
  3. ↑ Huang, C.; Kotzig, A.; Rosa, A. (1982), "Further results on tree labellings", Utilitas Mathematica 21: 31–48, MR 668845 .
  4. ↑ Morgan, David (2008), "All lobsters with perfect matchings are graceful", Bulletin of the Institute of Combinatorics and its Applications 53: 82-85 .
  5. ↑ 5.0 5.1 Gallian, Joseph A. (1998), "A dynamic survey of graph labeling", Electronic Journal of Combinatorics 5: Dynamic Survey 6, 43 pp. (electronic), MR 1668059 .
  6. ↑ Aldred, R. E. L.; McKay, Brendan D. (1998), "Graceful and harmonious labellings of trees", Bulletin of the Institute of Combinatorics and its Applications 23: 69–72, MR 1621760 .
  7. ↑ Fang, Wenjie (2010), A Computational Approach to the Graceful Tree Conjecture, arXiv:1003.3045 . See also Graceful Tree Verification Project
  8. ↑ Kotzig, Anton (1981), "Decompositions of complete graphs into isomorphic cubes", Journal of Combinatorial Theory. Series B 31 (3): 292–296, doi:10.1016/0095-8956(81)90031-9, MR 638285 .
  9. ↑ Weisstein, Eric W., "Graceful graph", MathWorld.

Additional reading

  • (K.Eshghi) Introduction to Graceful Graphs, Sharif University of Technology, 2002.
  • (U. N. Deshmukh and Vasanti N. Bhat-Nayak), New families of graceful banana trees - Proceedings Mathematical Sciences, 1996 - Springer
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.