Grace–Walsh–Szegő theorem

From Wikipedia, the free encyclopedia

In mathematics, the Grace–Walsh–Szegő coincidence theorem[1][2] is a result named after John Hilton Grace, Joseph L. Walsh, Gábor Szegő.

Statement

Suppose ƒ(z1, ..., zn) is a polynomial with complex coefficients, and that it is

  • symmetric, i.e. invariant under permutations of the variables, and
  • multi-affine, i.e. affine in each variable separately.

Let A be any simply connected open set in the complex plane. If either A is convex or the degree of ƒ is n, then for any 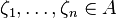\zeta _{1},\ldots ,\zeta _{n}\in A there exists 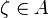\zeta \in A such that

f(\zeta _{1},\ldots ,\zeta _{n})=f(\zeta ,\ldots ,\zeta ).\,

Notes and references

  1. ↑ "A converse to the Grace–Walsh–Szegő theorem", Mathematical Proceedings of the Cambridge Philosophical Society, August 2009, 147(02):447–453. DOI:10.1017/S0305004109002424
  2. ↑ J. H. Grace, "The zeros of a polynomial", Proceedings of the Cambridge Philosophical Society 11 (1902), 352–357.


This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.