Goldstine theorem

From Wikipedia, the free encyclopedia

In functional analysis, a branch of mathematics, the Goldstine theorem, named after Herman Goldstine, asserts that the image of the closed unit ball 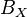$B_{X}$ of a Banach space $X$ under the canonical imbedding into the closed unit ball $B_{{X^{{**}}}}$ of the bidual space $X^{{**}}$ is weakly*-dense.

The conclusion of the theorem is not true for the norm topology, which can be seen by considering the Banach space of real sequences that converge to zero c₀, and its bi-dual space ℓ_∞.

Proof

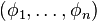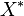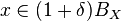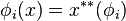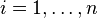Given an $x^{{**}}\in B_{{X^{{**}}}}$ , a tuple $(\phi _{1},\dots ,\phi _{n})$ of linearly independent elements of $X^{*}$ and a $\delta >0$ we shall find an $x\in (1+\delta )B_{{X}}$ such that $\phi _{i}(x)=x^{{**}}(\phi _{i})$ for every $i=1,\dots ,n$ .

If the requirement $\|x\|\leq 1+\delta$ is dropped, the existence of such an $x$ follows from the surjectivity of

$\Phi :X\to {\mathbb {C}}^{{n}},x\mapsto (\phi _{1}(x),\dots ,\phi _{n}(x)).$

Let now $Y:=\bigcap _{i}\ker \phi _{i}=\ker \Phi$ . Every element of $(x+Y)\cap (1+\delta )B_{{X}}$ has the required property, so that it suffices to show that the latter set is not empty.

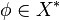Assume that it is empty. Then ${\mathrm {dist}}(x,Y)\geq 1+\delta$ and by the Hahn-Banach theorem there exists a linear form $\phi \in X^{*}$ such that 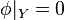$\phi |_{Y}=0$ , $\phi (x)\geq 1+\delta$ and $\|\phi \|_{{X^{*}}}=1$ . Then $\phi \in {\mathrm {span}}(\phi _{1},\dots ,\phi _{n})$ and therefore

$1+\delta \leq \phi (x)=x^{{**}}(\phi )\leq \|\phi \|_{{X^{*}}}\|x^{{**}}\|_{{X^{{**}}}}\leq 1,$

which is a contradiction.

v t e Functional analysis

Local Notions on Sets	Absolutely convex Absorbing Balanced Bounded Cones (Linear, Convex cone) Convex Radial Star-shaped Symmetric

Types of TVSs	Banach Barrelled Bornological Brauner F-space Finite-dimensional Fréchet (Tame) Hilbert LF Locally convex Mackey Montel Nuclear Normed (Norm) Reflexive Riesz Smith Stereotype Topological tensor product (of Hilbert spaces) Webbed

Spaces of Maps	Dual space Dual topology Operator topologies Strong Topology (Polar, Operator) Topology of uniform convergence Weak topology (operator) Ultrastrong topology Ultraweak topology

Types of Linear operators	Adjoint Bilinear (form) Bounded (Unbounded) Closed Continuous (Discontinuous) Compact Fredholm Hilbert–Schmidt Functionals (Positive) Normal Nuclear Self-adjoint Strictly singular Trace class Transpose Unitary

Operations on Sets	Algebraic interior (core) Interior Minkowski addition Polar

Banach Algebras	C-algebras Spectrum (of a C-algebra, Spectral radius) Spectral theory

Important Theorems	Banach–Alaoglu Banach–Saks Banach–Mazur Bessel's inequality Cauchy–Schwarz inequality Closed range Closed graph Eberlein–Šmulian Freudenthal spectral Gelfand–Mazur Goldstine Hahn–Banach (Hyperplane separation) Kakutani fixed-point Lomonosov's Invariant Subspace Mackey–Arens Mazur's lemma M. Riesz extension Open mapping Parseval's identity Schauder fixed-point

Analysis	Bochner space Derivatives (Fréchet derivative, Gâteaux derivative, Functional, Holomorphy) Differentiation in Fréchet spaces Integrals (Bochner, Dunford, Gelfand–Pettis, Regulated, Weak) Functional calculus Inverse function theorem (Nash–Moser theorem) Vector measure

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.

Goldstine theorem

Proof

See also