Global square
From Wikipedia, the free encyclopedia
Global square is an important concept in set theory, a branch of mathematics. It has been introduced by Ronald Jensen in his analysis of the fine structure of the constructible universe L. According to Ernest Schimmerling and Martin Zeman, Jensen's square principle and its variants are ubiquitous in set theory.[1]
Definition
Define Sing to be the class of all limit ordinals which are not regular. Global square states that there is a system  satisfying:
satisfying:
Variant relative to a cardinal
Jensen introduced also a local version of the principle.[2] If
 is an uncountable cardinal,
then
is an uncountable cardinal,
then  asserts that there is a sequence
asserts that there is a sequence 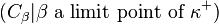 satisfying:
satisfying:
-
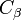 is a club set of
is a club set of  .
. - If
 , then
, then 
- If
 is a limit point of
is a limit point of 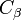 then
then 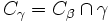
Notes
- ↑ Ernest Schimmerling and Martin Zeman, Square in Core Models, The Bulletin of Symbolic Logic, Volume 7, Number 3, Sept. 2001
- ↑ Jech, Thomas (2003), Set Theory: Third Millennium Edition, Springer Monographs in Mathematics, Berlin, New York: Springer-Verlag, ISBN 978-3-540-44085-7, p. 443.
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.
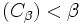
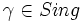 and
and