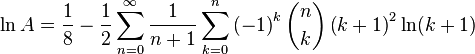Glaisher–Kinkelin constant
In mathematics, the Glaisher–Kinkelin constant or Glaisher's constant, typically denoted A, is a mathematical constant, related to the K-function and the Barnes G-function. The constant appears in a number of sums and integrals, especially those involving Gamma functions and zeta functions. It is named after mathematicians James Whitbread Lee Glaisher and Hermann Kinkelin.
Its approximate value is:
The Glaisher–Kinkelin constant  can be given by the limit:
can be given by the limit:
where 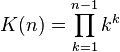 is the K-function. An equivalent form involving the Barnes G-function, given by
is the K-function. An equivalent form involving the Barnes G-function, given by ![G(n)=\prod _{{k=1}}^{{n-2}}k!={\frac {\left[\Gamma (n)\right]^{{n-1}}}{K(n)}}](/2014-wikipedia_en_all_02_2014/I/media/f/5/3/6/f53602e8f206563c54b5dee9b4eb9bf2.png) where
where  is the gamma function is:
is the gamma function is:
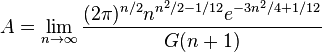 .
.
The Glaisher–Kinkelin constant also appears in the Riemann zeta function, such as:
where  is the Euler–Mascheroni constant.
is the Euler–Mascheroni constant.
Some integrals involve this constant:
A series representation for this constant follows from a series for the Riemann zeta function given by Helmut Hasse.
References
- Guillera, Jesus; Sondow, Jonathan (2005). "Double integrals and infinite products for some classical constants via analytic continuations of Lerch's transcendent". arXiv:math.NT/0506319.
- Guillera, Jesus; Sondow, Jonathan (2008). "Double integrals and infinite products for some classical constants via analytic continuations of Lerch's transcendent". Ramanujan Journal 16 (3): 247–270. doi:10.1007/s11139-007-9102-0. (Provides a variety of relationships.)
- Weisstein, Eric W., "Glaisher–Kinkelin Constant", MathWorld.
- Weisstein, Eric W., "Riemann Zeta Function", MathWorld.

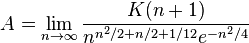
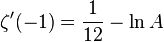
![\sum _{{k=2}}^{\infty }{\frac {\ln k}{k^{2}}}=-\zeta ^{{\prime }}(2)={\frac {\pi ^{2}}{6}}\left[12\ln A-\gamma -\ln(2\pi )\right]](/2014-wikipedia_en_all_02_2014/I/media/5/1/e/7/51e72c50a5d86079e32b7c21bd083fc9.png)