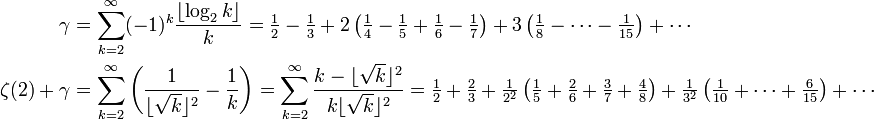Giovanni Vacca

From Wikipedia, the free encyclopedia

For the Italian physiologist, see Giovanni Vacca (doctor).

Giovanni Vacca

Born	(1872-11-18)18 November 1872 Genoa, Italy
Died	6 January 1953(1953-01-06) (aged 80) Rome, Italy
Nationality	Italian
Fields	Mathematics

Giovanni Enrico Eugenio Vacca (18 November 1872 – 6 January 1953) was an Italian mathematician, Sinologist and historian of science.

Vacca studied mathematics and graduated from the University of Genoa in 1897 under the guidance of G. B. Negri. He was a politically active student and was banished for that from Genoa in 1897. He moved to Turin and became an assistant to Giuseppe Peano. In 1899 he studied, at Hanover, unpublished manuscripts of Gottfried Wilhelm Leibniz, which he published in 1903. Around 1898 Vacca became interested in Chinese language and culture after attending a Chinese exhibition in Turin. He took private lessons of Chinese and continued to study it at the University of Florence. Vacca then traveled to China in 1907–8 and defended a PhD in Chinese studies in 1910. In 1911, he became a lecturer in Chinese literature at the University of Rome. In 1922, he moved to Florence and taught Chinese literature and language at university until 1947. ^[1]

The interests of Vacca were almost equally split between mathematics, Sinology and history of science, with a corresponding number of papers being 38, 47 and 45. In 1910, Vacca developed a complex number iteration for pi:^[2]

$x_{0}=i,\quad x_{{n+1}}={\frac {x_{n}+|x_{n}|}2},\qquad \lim _{{n\to \infty }}x_{n}={\frac 2\pi }.$

The calculation efficiency of these formulas is significantly worse than of the modern Borwein's algorithm – they converge by only about half a decimal point with each iteration.

Vacca published his two major contributions to mathematics in 1910 and 1926, on series expansion (later named Vacca series) of the Euler constant. They are, respectively

${\begin{aligned}\gamma &=\sum _{{k=2}}^{\infty }(-1)^{k}{\frac {\left\lfloor \log _{2}k\right\rfloor }{k}}={\tfrac 12}-{\tfrac 13}+2\left({\tfrac 14}-{\tfrac 15}+{\tfrac 16}-{\tfrac 17}\right)+3\left({\tfrac 18}-\cdots -{\tfrac 1{15}}\right)+\cdots \\\zeta (2)+\gamma &=\sum _{{k=2}}^{\infty }\left({\frac 1{\lfloor {\sqrt {k}}\rfloor ^{2}}}-{\frac 1{k}}\right)=\sum _{{k=2}}^{{\infty }}{\frac {k-\lfloor {\sqrt {k}}\rfloor ^{2}}{k\lfloor {\sqrt {k}}\rfloor ^{2}}}={\tfrac 12}+{\tfrac 23}+{\tfrac 1{2^{2}}}\left({\tfrac 15}+{\tfrac 26}+{\tfrac 37}+{\tfrac 48}\right)+{\tfrac 1{3^{2}}}\left({\tfrac 1{10}}+\cdots +{\tfrac 6{15}}\right)+\cdots \end{aligned}}$

Vacca noted in 1910 that:^[3]

There is some hope that this series can be of some use in the proof of the irrationality of $\gamma$ , a very difficult problem, proposed, but not resolved, in the Correspondence, recently published, between Hermite und Stieltjes.

References

↑ O'Connor, John J.; Robertson, Edmund F., "Giovanni Vacca", MacTutor History of Mathematics archive, University of St Andrews .
↑ G. Vacca. A new analytical expression for the number π and some historical considerations, Bulletin of the American Mathematical Society (Ser. 2), 1910, vol.16, pp. 368–369
↑ James Joseph Sylvester; James Whitbread Lee Glaisher (1910). The Quarterly journal of pure and applied mathematics. J.W. Parker. p. 364. Retrieved 16 August 2011.

Authority control	VIAF: 90248804 GND: 117324841 ICCU: IT\ICCU\MILV\176884

Persondata
Name	Vacca, Giovanni Enrico Eugenio
Alternative names
Short description	Italian mathematician
Date of birth	18 November 1872
Place of birth	Genoa, Italy
Date of death	6 January 1953
Place of death	Rome, Italy

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.