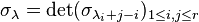Giambelli's formula

From Wikipedia, the free encyclopedia

In mathematics, Giambelli's formula, named after Giovanni Giambelli, expresses Schubert classes in terms of special Schubert classes, or Schur functions in terms of complete symmetric functions.

It states

$\displaystyle \sigma _{\lambda }=\det(\sigma _{{\lambda _{i}+j-i}})_{{1\leq i,j\leq r}}$

where σ_λ is the Schubert class of a partition λ.

Giambelli's formula is a consequence of Pieri's formula. The Porteous formula is a generalization to morphisms of vector bundles over a variety.

References

Fulton, William (1997), Young tableaux, London Mathematical Society Student Texts 35, Cambridge University Press, ISBN 978-0-521-56144-0; 978-0-521-56724-4 Check |isbn= value (help), MR 1464693
Sottile, Frank (2001), "Schubert calculus", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.